Quelques surfaces classiques.

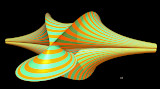
Dôme de Bohème Equation (x^2+y^2+z^2-a^2-b^2)^2-4*(a^2-x^2)*(b^2-y^2) Le fichier Povray à télécharger ICI a =1 ; b = 1 fond bleu   en 800x600 fond blanc   en 800x600 a =1.5 ; b = 1 fond bleu   en 800x600 fond blanc   en 800x600 Début	Conoïde de Plucker Le fichier Povray à télécharger ICI   en 800x600
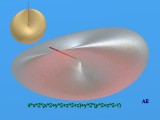
Surface de Steiner ou Cross-Cap Equation : (x^2+y^2+z^2-a^2-b^2)^2-4*(a^2-x^2)*(b^2-y^2) Le fichier Povray à télécharger ICI fond bleu   en 800x600         fond blanc   en 800x600 Début	Surface de Cassini Equation : z^2+1+2*y^2+y^4-2*x^2+2*x^2*y^2+x^4; Le fichier Povray à télécharger ICI fond bleu   en 800x600 fond blanc   en 800x600
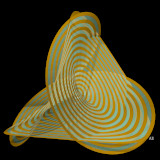
Surface de Steiner-Romane Equation : x^2*y^2+x^2*z^2+y^2*z^2+2*a*x*y*z ; Le fichier Povray à télécharger ICI   Début	Surface minimale de Bour Equations : x = uu*cos(vv)-uu*uu/2*cos(2*vv) y = -uu*sin(vv)-uu*uu/2*sin(2*vv) z = 4/3*uu*sqrt(uu)*cos(3*vv/2) Le fichier Povray à télécharger ICI
Surface de Kuen       Equation 1 : x = 2*(cos(u)+u*sin(u))*sin(v)/(1+u*u*sin(v)*sin(v)) y = 2*(sin(u)-u*cos(u))*sin(v)/(1+u*u*sin(v)*sin(v)) z = log(tan(v/2))+2*cos(v)/(1+u*u*sin(v)*sin(v))       Equation 2 : x = 2*(cos(u)+u*sin(u))*cosh(v)/(u^2+cosh(v)^2) y = 2*(sin(u)-u*cos(u))*cosh(v)/(u^2+cosh(v)^2) z = v-sinh(2*v)/(u^2+cosh(v)^2) Le fichier Povray à télécharger ICI La forme classique tricolore   en 800x600         bicolore   en 800x600         Génératrices   en 800x600 Autre forme fond bleu   en 800x600         fond blanc   en 800x600 Début
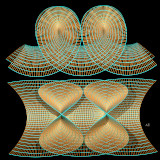
Surface de Richmond Equations paramétriques : cx = 1/6*(-3*u-u^5+2*u^3*v^2+3*u*v^4)/(u^2+v^2) cy = 1/6*(-3*v+v^5+2*u^2*v^3-3*v*u^4)/((u^2+v^2)) cz := u L'image Povray a été tracée à l'aide de l'équation implicite (voir fichier Povray). Le fichier Povray à télécharger ICI fond bleu   en 800x600         fond blanc   en 800x600 Début	Surface de Catalan Equation : x = uu-sin(uu)*cosh(vv) y = 1-cos(uu)*cosh(vv) z = 4*sin(1/2*uu)*sinh(vv/2) Le fichier Povray à télécharger ICI     en 800x800                 en 800x800
Trompette de Gabriel Equation : z = 1/r ; Le fichier Povray à télécharger ICI fond bleu   en 800x600         fond blanc   en 800x600 Début	Entonnoir Equation : z = ln(r)/2 ; Le fichier Povray à télécharger ICI fond bleu   en 800x600         fond blanc   en 800x600
Surface de Boy Le fichier Povray à télécharger ICI fond bleu   en 800x600 fond blanc   en 800x600 en 800x600 en 800x600 Début	Chapeau Equation : x^2+y^2+z^3-3 Le fichier Povray à télécharger ICI fond bleu   en 800x600
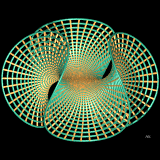
Chapeaux chinois Eéquations paramétriques : x=cos(u)*cos(v); y=cos(u)*sin(v); z:=sin(u)^n; Le fichier Povray à télécharger ICI Pour n pair : 2, 4, 6, 8 fond bleu   en 800x600 fond blanc   en 800x600 Pour n impair : 3, 5, 7 fond bleu   en 800x600 fond blanc   en 800x600 Début	Surface de Enneper Le fichier Povray à télécharger ICI   en 800x800  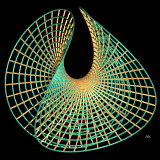 en 800x800   en 800x800   en 800x800   zoom
Parapluie de Whitney Le fichier Povray à télécharger ICI   en 800x600 Début	Surface de Hunt Le fichier Povray à télécharger ICI   en 800x600
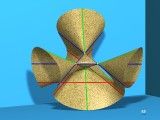
Surface de Cayley Le fichier Povray à télécharger Cayley type 1 ICI Le fichier Povray à télécharger Cayley type 2 ICI   en 800x600   en 800x600 Début	Surface de Dini Le fichier Povray à télécharger ICI fond bleu   en 800x600         fond blanc   en 800x600
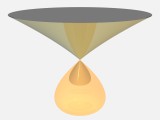
Amphore Equation : (x^2 + 0.02*y^2 + z^2)^2 + 4*(x^2 + z^2)*y Le fichier Povray à télécharger ICI fond bleu   en 800x600         fond blanc   en 800x600 Début	Luminaire Equation : -0.2*x^3 + 1.4*x^2 + 0.01*x-y^2-z^2 Le fichier Povray à télécharger ICI   en 800x600
Flute à champagne a*x*y^2 + a*x*z^2+ b*x^2+ y^2+c*y+z^2-0.1 Equation : (x + 1 )*(y^2 + z^2) - x^2 + y - 0.1 Le fichier Povray à télécharger ICI   en 800x600           avec les bulles Début	Surface de Barth Equation : z^6-5*(x^2+y^2)*z^4+5*(x^2+y^2)^2*z^2-2*(x^4-10*x^2*y^2+5*y^4)*x*z+(5/4)*(x^2+y^2+z^2)^2-(5/2)*x^2-(5/2)*y^2-(5/2)*z^2+5/4   en 800x800
Trèfle, noeud torique Le fichier Povray de "trèfle" à télécharger ICI Le fichier Povray de "noeud torique" à télécharger ICI   en 800x600   en 800x600   en 800x600 Début
Ellipsoïde astroïdale Les fichiers Povray à télécharger ICI et ICI l'ellipsoïde astroïdale l'ellipsoïde astroïdale approchée par une famille de triangles(*)   en 800x600     144 triangles en 800x600   320 triangles en 800x600   19300 triangles en 800x600 (*) La famille de triangles ABC, A sur Ox, B sur Oy, C sur Oz, tels que la distance de O à son centre de gravité soit constante est enveloppée par un ellipsoïde astroïdale. La partie visible des triangles de la famille, dans les images ci-dessus, approche sensiblement son enveloppe, c'est-à-dire l'ellispsoïde astroïdale. Début
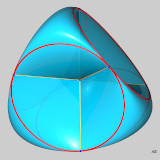
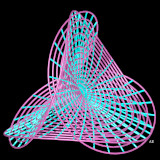
Tétraèdre de Reuleaux Cette surface de "largeur" constante est constituée de l'intersection de quatre sphères centrées aux quatre sommets d'un tétraèdre régulier et de rayon l'arête de ce tétraèdre. Le segment de normale en tout point régulier intérieur à la surface a pour longueur l'arête du tétraèdre. Attention ! La surface n'est pas de "diamètre" constant (le maximum de distance d'un point M de la surface à un point variable de cette surface n'est pas indépendant de M -- le diamètre varie entr L et L*1.024.. ) Le fichier Povray à télécharger ICI On peut aussi considérer le volume engendré par un triangle de Reuleaux(anguleux ou arrondi - voir Maple/courbes auto-parallèles -) en tournant autour d'un de ces axes de symétrie. Le diamètre est alors constant. Le fichier Povray à télécharger ICI Tétraèdre de Reuleaux fond bleu   en 800x600 fond blanc   en 800x600 volumes de révolution Triangle anguleux fond bleu   en 800x600 fond blanc   en 800x600 volumes de révolution Triangle arrondi fond bleu   en 800x600 fond blanc   en 800x600 Début

---