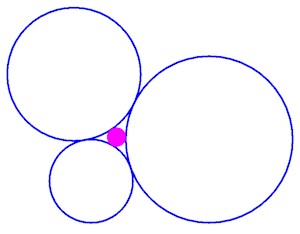
3 cercles tangents 2 à 2
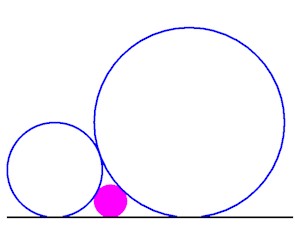
2 cercles tangents et tangents à un côté
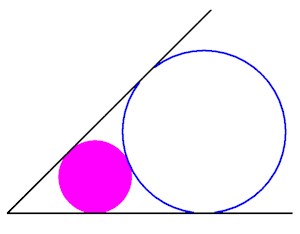
cercle tangent à 2 côtés
Empilements apolloniens de cercles
Sur des sujets voisins, voir les pages :
cercles-sphères Apollonius
badernes sphériques
cercles tangents
Empilements apolloniens de cercles dans un polygône
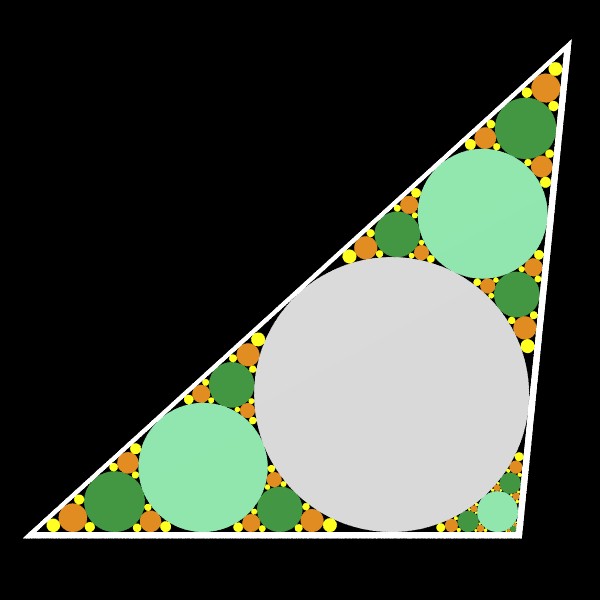
On part d'une disposition élémentaire de cercles intérieurs à un polygône, tangents entre eux deux à deux et éventuellement tangents à un ou plusieurs cotés du polygône tels que ci-dessous.
Dans chaque espace entre trois cercles deux à deux tangents ou deux cercles tangents et tangents à un coté ou un cercle tangent à deux cotés adjacents, on insére un cercle tangent aux trois composants :
 3 cercles tangents 2 à 2 |
 2 cercles tangents et tangents à un côté |
 cercle tangent à 2 côtés |
|
départ : triangle avec son cercle inscrit |
|
 | 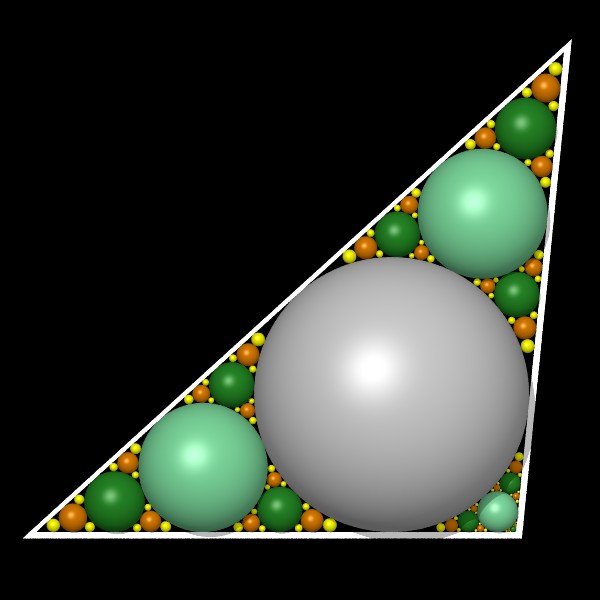 |
|
départ : triangle avec trois cercles tangents deux à deux |
|
 | 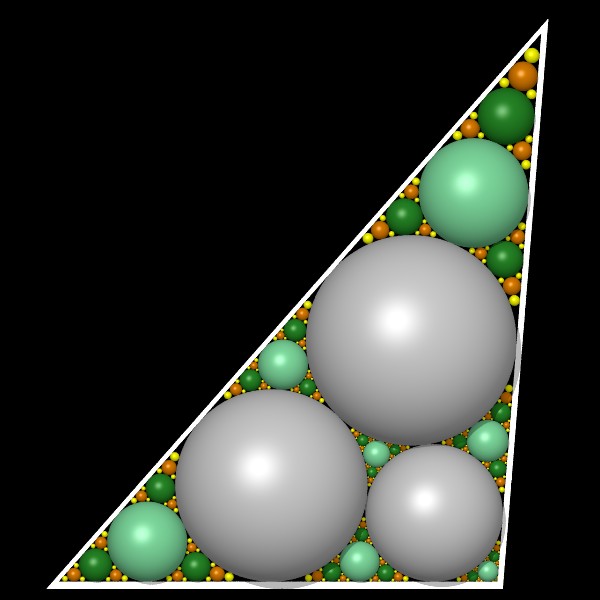 |
|
départ : carré avec quatre cercles égaux et un cercle central |
|
 | 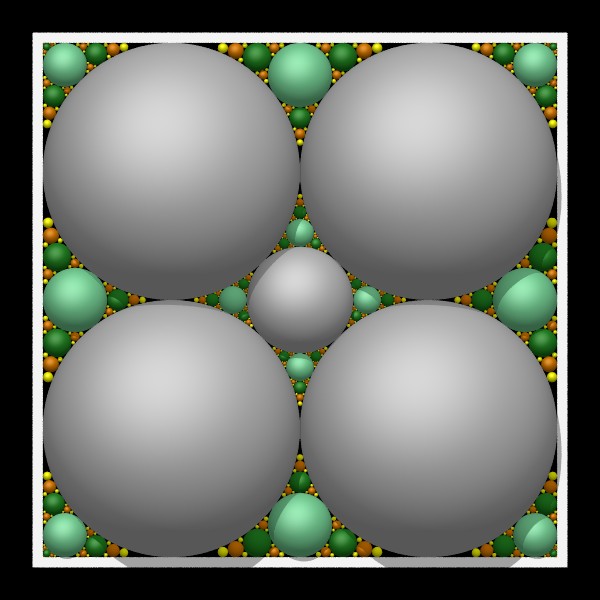 |
|
départ : carré avec quatre cercles inégaux |
|
 |  |
 Début
Début