II. Inversion d'une série de cercles tangents deux à deux et tangents à deux cercles concentriques
Inversions de cercles - Cercles et sphères d'Apollonius
Sur des sujets voisins, voir les pages :
empilements apolloniens
badernes spheriques
cercles tangents
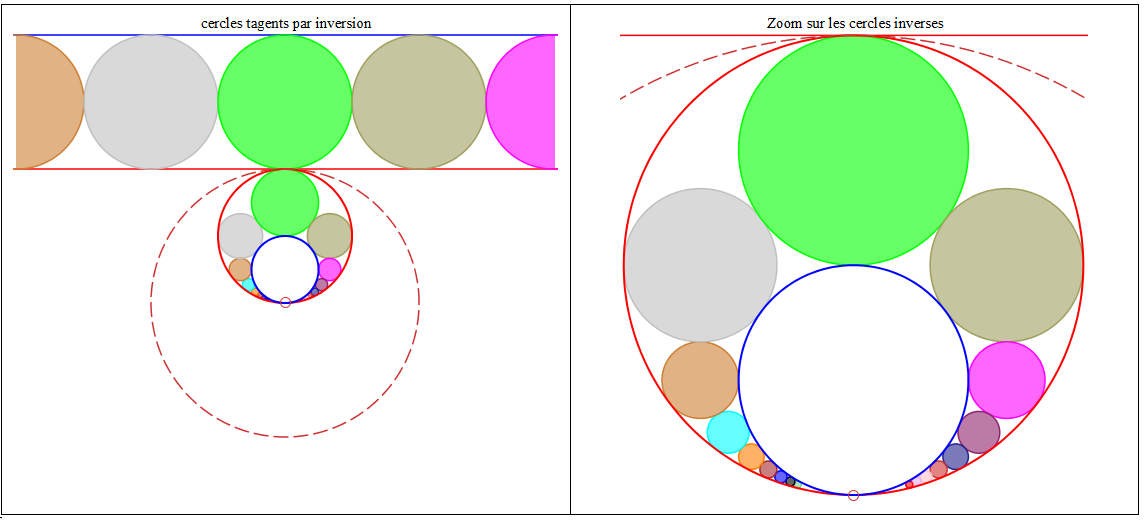
I. Inversion d'une série de cercles tangents deux à deux et tangents à deux droites parallèles
Si l'on considère une inversion de pôle I non situé sur les droites, celles-ci sont transformées en deux cerclmes (C1) et (C2) passant par I et la série de cercles en des cercles tangents à (C1) et (C2)

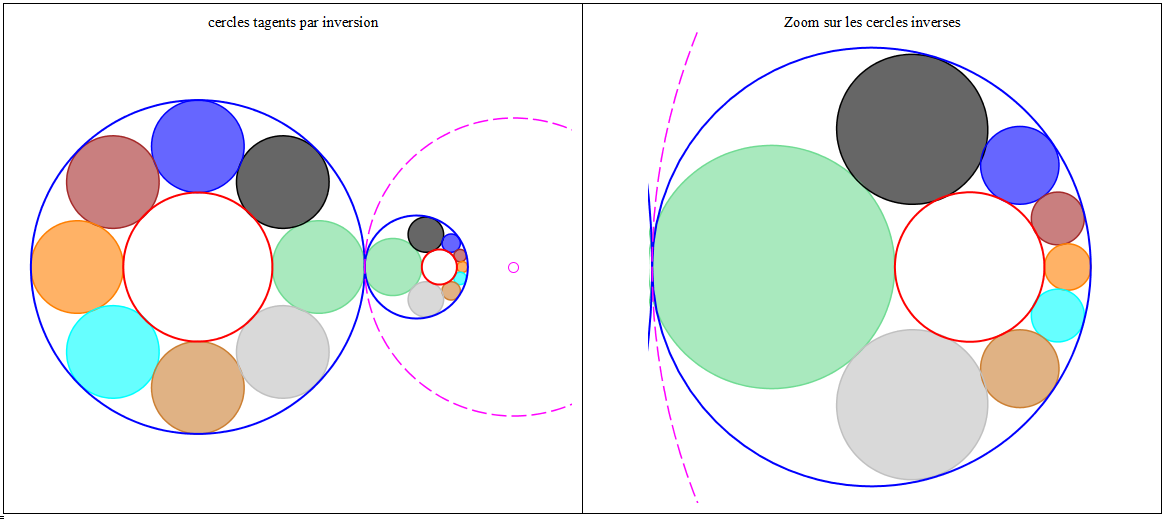
II. Inversion d'une série de cercles tangents deux à deux et tangents à deux cercles concentriques
Si l'on considère une inversion de pôle I non situé sur les cercles, ceeux-ci sont transformées en deux cerclmes (C1) et (C2) non concentriques et la série de cercles en une série de Steiner
III. Cercles d'Apollonius
Soit un polygone régulier à N cotés de longueur 2r, de centre Im, de sommets S(i)=r/sin(Pi/N)*[cos(2*Pi*(i-1)/N), sin(2*Pi*(i-1)/N)] et les N cercles C(i) de rayon r centrés en ces sommets pour i=1..N.
On appelle Ce le cercle circonscrit à ces cercles, donc de rayon R=r+r/sin(Pi/N) et Cm le cercle "inscrit" de rayon R-2r.
Pour i=1..N, soit I(i) l'inversion laissant Ce, les deux cercles contigus C(i) et C( (i mod N)+1) et le cercle Ce invariants globalement.
Soit Im l'inversion de centre O laissant les cercles C(i) invariants globalement ; elle transforme le cercle Ce en le cercle Cm.
J'ai tracé en rouge les cercles d'inversion.
Dans le programe Maple, j'ai fait une hmothétie telle que pour tout N, le grand cercle Ce ait pour rayon 1.
Etape 1 : (E1) étant la réunion de tous les cercles précédents, on prend la réunion (F) des images de (E1) par les N inversions I(i) puis la réunion (E2) de (F) et de l'image de (F) par Im.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Début
Début