cercles-sphères Apollonius
empilements apolloniens
cercles tangents
Empilements apolloniens de cercles sur une sphère
1. BADERNES ETOILEES : Réitération d'inversions de pôles les sommets d'un polyèdre régulier
J'ai considéré un polyèdre régulier ( tétraèdre, cube, octaèdre ...) et la sphère S0 tangente à ses arêtes en leur milieu. Les faces coupent ainsi cette sphère selon des cercles égaux et tangents.
Je considère les inversions Ci centrées aux sommets Ai du polyèdre et laissant globalement invariante la sphère S0.
Je fais subir à tous les cercles les inversions Ci (sauf ceux invariants par Ci ) : j'obtiens une nouvelle famille (F1) de cercles tracés sur la sphère S0.
Je recommence l'opération avec (F1) et ainsi de suite (F2), ...
On obtient ainsi des pavages de la sphère par des "badernes étoilées" gauches.
2. BADERNES CIRCULAIRES : Réitération d'inversions de pôles sur les axes des faces d'un polyèdre régulier
J'ai considéré un polyèdre régulier ( tétraèdre, cube, octaèdre ...) et la sphère S0 tangente à ses arêtes en leur milieu. Les faces coupent ainsi cette sphère selon des cercles égaux et tangents.
Je considère les inversions Ci dont les pôles sont sur les axes des faces du polyèdre et laissant globalement invariante la sphère S0.
Je procède ensuite comme pour la méthode 1 ...
On obtient ainsi des pavages de la sphère par des "badernes circulaires" gauches.( situées dans les grandes calottes des pavages 1)
Dans ce paragraphe, les images des seconde et quatrième colonnes des tableaux sont des images en relief à regarder avec des lunettes rouge-cyan.
|
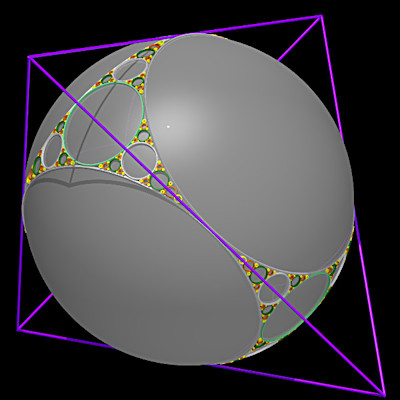
Baderne étoilée du tétraèdre |
Baderne circulaire du tétraèdre |
||
 |  |
 |  |
|
Baderne étoilée du cube |
Baderne circulaire du cube |
||
 |
 |
 |  |
|
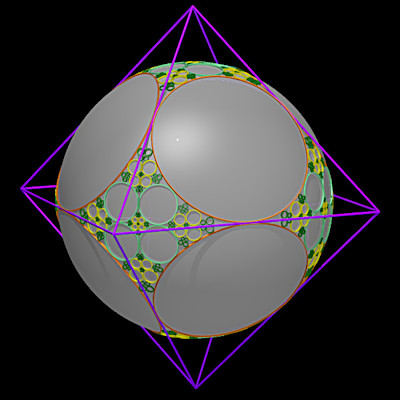
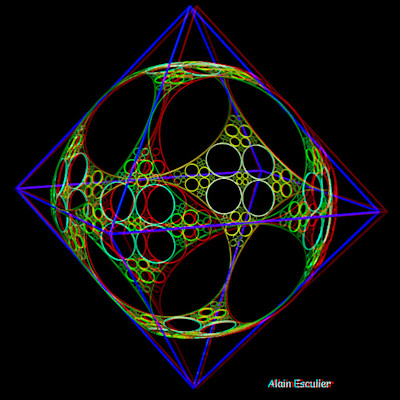
Baderne étoilée de l'octaèdre |
Baderne circulaire de l'octaèdre |
||
 |
 |
 |  |
|
Baderne étoilée du dodécaèdre |
Baderne circulaire du dodécaèdre |
||
 |
 |
 |  |
|
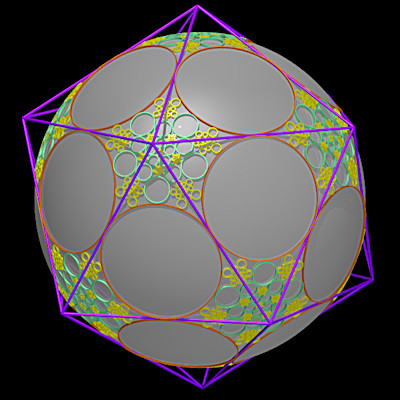
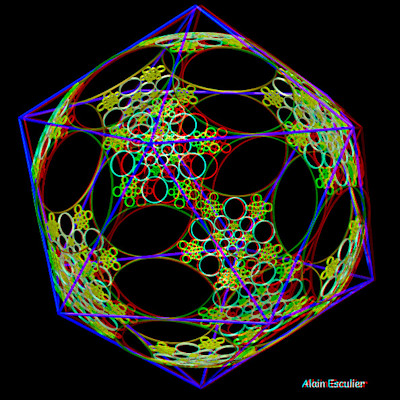
Baderne étoilée de l'icosaèdre |
Baderne circulaire de l'icosaèdre |
||
 |
 |
 |  |
|
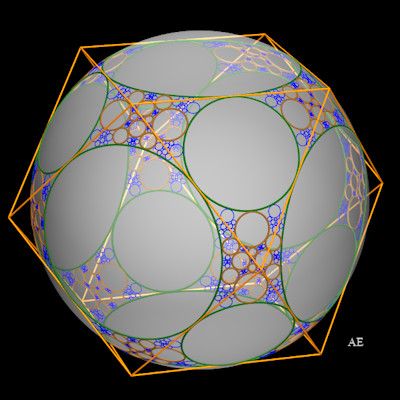
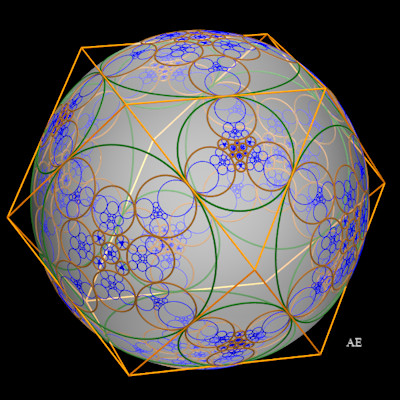
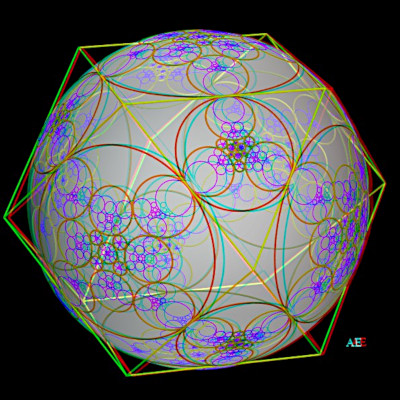
Baderne étoilée du cuboctaèdre |
Baderne circulaire du cuboctaèdre |
||
 |  |
 |  |
|
Baderne étoilée du grand rhombicuboctaèdre |
Baderne circulaire du grand rhombicuboctaèdre |
||
 |  |
 |  |
3. Projection stéréographique inverse d'une baderne ou d'un empilement apollonien du plan sur une sphère
Cette méthode très simple à mettre en oeuvre est donc beaucoup plus riche puisque les empilements de cercles du plan sont très divers.
On peut ensuite faire subir diverses rotations sur la sphère à l'image de l'empilement ainsi obtenue.
|
Départ : baderne plane avec 4 cercles égaux + rotations |
Départ : baderne plane avec 4 cercles égaux + rotations |
||
 |
 |
 |
 |
|
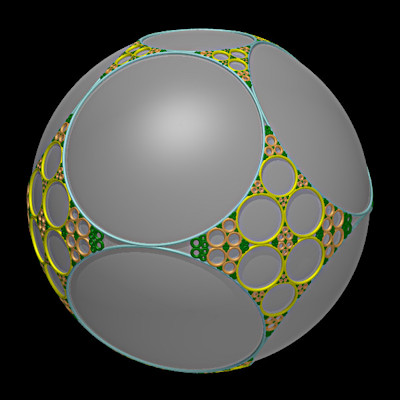
Départ : baderne plane avec 4 cercles égaux + symétrie |
Départ : badernes imbriquées + symétrie |
||
 |
 |
 |
 |
|
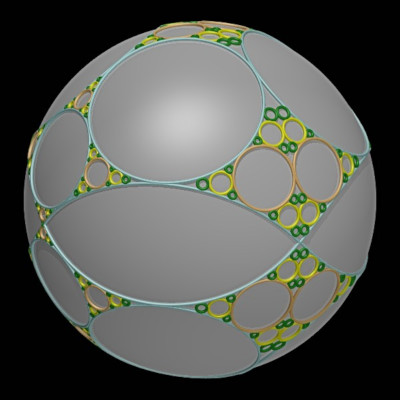
Départ : badernes imbriquées + symétrie |
>
Départ : empilement Apollonien dans un carré + symétrie |
||
 |
 |
 |
 |
 Début
Début