Nombres figurés

Nombres figurés

I. Nombres polygonaux centrés

Soit (P1) un polygone régulier à N cotés de centre O.
k étant un entier positif, on considère les polygones (Pi) déduits de (P1) par les homthéties de centre O de rapport (k-i)/(k-1), i variant de 2 à k. (Pk) est réduit au point O.

Un nombre N-gonal centré d'ordre k est représenté par l'ensemble des points disposés régulièrement sur les polynomes (Pi) pour i variant de 1 à k-1 :
1. (k-i+1) points régulièrement espacés sur chaque coté du polygone (Pi), pour i variant de 1 à k-1 soit N*(k-i) points sur (Pi).
2. le point O correspondant à (Pk).

Le nombre N_gonal d'ordre k est donc:
NF(N,k) = sum( N*(k-i),i=1..k-1) + 1 = N*k*(k-1)/2 + 1.

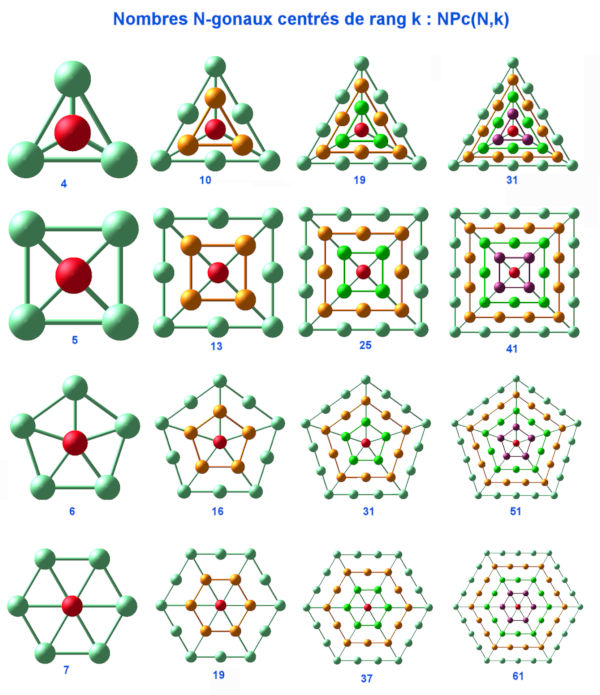
NPc(N,k)= N*k*(k-1)/2 + 1:

II. Nombres polygonaux gnomoniques

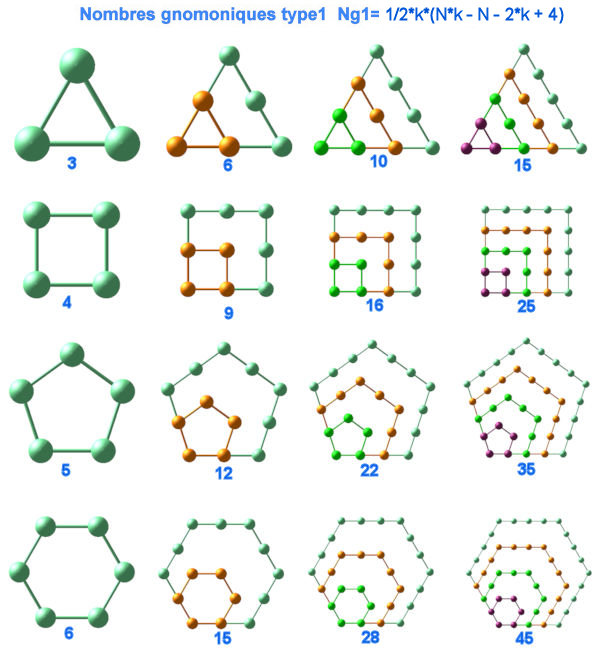
1. Nombres polygonaux gnomoniques type 1

Soit (P1) un polygone régulier à N cotés et p1 l'un de ses sommets.
k étant un entier positif, on considère les polygones (Pi) déduits de (P1) par les homthéties de centre p1 de rapport (k-i)/(k-1), i variant de 2 à k-1.

Un nombre N-gonal centré d'ordre n est représenté par l'ensemble des points suivants :
1. (k-i+1) points régulièrement espacés sur chaque coté du polygone (Pi), pour i variant de 1 à k-1 soit N*(k-i) points au total.
Pour i>1, le polynome (Pi) a (2*k-2*i-1) points confondus avec (P1).

Le nombre N_gonal gnomonique d'ordre k est donc:
Ngtype1(N,k) = 1/2*k*(N*k - N - 2*k + 4)

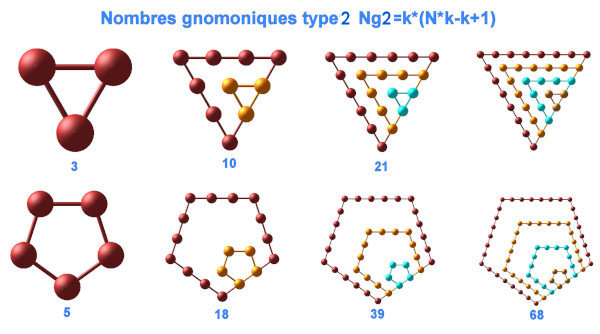
2. Nombres polygonaux gnomoniques type 2
De même que précédemment avec les polygones (Pi) qui sont déduits de (P1) par les homthéties de centre p1 milieu d'une arête de (P1) de rapport (2*k-2*i)/(2*k-2), i variant de 1 à k-1.
(2*(k-i)) points sont régulièrement espacés sur les arêtes des polygones (Pi)

Le nombre N_gonal gnomonique d'ordre k est donc:
Ngtype2 = k*(N*k-k+1)):
On retrouve les suites obtenues dans l'encyclopédie des suites OEIS.org

3. Nombres polygonaux gnomoniques type 3
De même que précédemment avec les polygones (Pi) qui sont déduits de (P1) par les homthéties de centre p1 milieu d'une arête de (P1) de rapport (2*k-2*i)/(2*k-2), i variant de 1 à k-1.
(2*(k-i) +1) points sont régulièrement espacés sur les arêtes des polygones (Pi)

Le nombre N_gonal gnomonique d'ordre k est donc:
Ngtype3 =(k + 1)*(N*k - k + 1):
On retrouve les suites obtenues dans l'encyclopédie des suites OEIS.org

III. Nombres pyramidaux centrés

On considère une pyramide de base (P0) un polygone représentant un nombre N-gone centré de rang k et de k étages(Pi) réguliers représentant un nombre N-gone centré de rang k-i pour i variant 0 à k. (Pk) réduit à un point S, sommet de la pyramide.
Donc le nombre pyramidal N-gonal de rang k Npyr(N,k) = 1/6*(k + 1)*(N*k^2 + 2*N*k + 6)

nombres pyramidaux centrés à base hexagonale
Rang k = 1 ; Npyrc(6,1) = 8 anaglyphe	Rang k = 2 ; Npyrc(6,2) = 27 anaglyphe	Rang k = 3 ; Npyrc(6,3) = 64 anaglyphe

IV. Nombres pyramidaux gnomoniques

On considère une pyramide de base (P0) un polygone représentant un nombre N-gone gnomonique de rang k et de k étages(Pi) réguliers représentant un nombre N-gone gnomonique de rang k-i pour i variant 0 à k. (Pk) réduit à un point S, sommet de la pyramide.
Donc le nombre pyramidal N-gonal de rang k Npyrg(N,k) = 1/6*(k + 2)*(3 + (N - 2)*k)*(k + 1)

nombres pyramidaux gnomoniques à base carrée
Rang k = 1 ; Npyrg(4,1) = 5 anaglyphe	Rang k = 2 ; Npyrg(4,2) = 14 anaglyphe	Rang k = 3 ; Npyrg(6,3) = 30 anaglyphe

IV. Nombres polyédriques centrés

Soit un polyèdre régulier (P1) de centre O et k un entier positif.
Soient (Pi) les polyèdres déduits de (P1) par homothétie de centre O et de rapport (k-i+1)/k pour i variant de 1 à k ; pour i=k+1, on considère que l'on obtient le point O.
Chaque face d'un polyèdre (Pi) réprésentant un nombre polygonal centré de rang k-i+1, la somme de tous ces nombres plus 1 est le nombre polyèdrique d'ordre k associé au type de polyèdre.

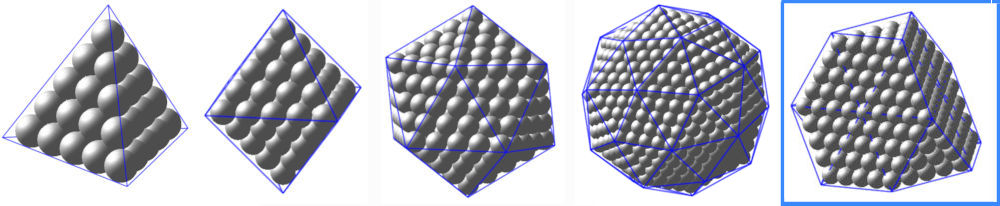
nombres tétraédriques
anaglyphe	anaglyphe	anaglyphe

nombres cuboctadriques
anaglyphe	anaglyphe	anaglyphe

nombres dodécaédriques
anaglyphe	anaglyphe	anaglyphe

V. Nombres polyèdriques gnomoniques

Les polyèdres successifs ont un sommet commun et les faces respéctives ayant ce sommet sont coplonaires.
Les faces d'un quelconque de ces polyèdres représentent un nombre polygonal gnomonique.

nombres gnomoniques polyèdriques
nombre cubique 3 anaglyphe	nombre octaédrique 3 anaglyphe	nombre dodécaédrique 2 anaglyphe

VI. Nombres polyédriques : cas particulier des polyèdres à faces équilatérales

Pour une face en triangle équilatéral de coté a , on peut considérer le réseau hexagonal de pas a/n de ce triangle. Les sphères de rayon a/(2*n) centrées aux sommets de ce réseau sont tangentes à leurs voisines.

En appliquant cela au tétraèdre, octaèdre, icosaèdre, pentakidodécaèdre,... on obtient les nombres polyédriques correspondants.
On peut faire de même à une face qui peut se décomposer en triangles équilatéraux, par exemple, le tétrèdre tronqué.