GéodesFleurs

On part d'une géode (G1) à faces triangulaires.
        1. Par dualité appliquée à (G1), on obtient une géode (G2) à faces hexagonales et 12 faces pentagonales (géode de type Goldberg ).
        2. Par adoucissement( polyèdre camus associé ) de (G2), on obtient une géode (G3) à faces triangulaires, pentagonales et hexagonales.
        3. Par dualité appliquée à (G3), on obtient une "géode fleurs" (G4) à fleurs hexagonales à 6 pétales et 12 fleurs pentagonales à 5 pétales.

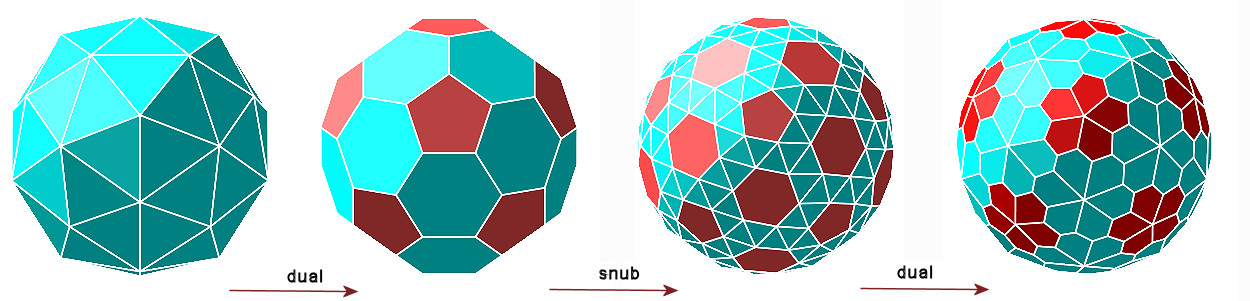
géode 60 faces (pentakidodécaèdre) dualGEODE 32 faces ; 12 pentagones ; 20 hexagones ; snubGEODE 92 faces triangulaires, 20 faces hexagonales, 12 pentagonales géodeFleurs : 12 fleurs 5 pétales ; 20 fleurs 6 pétales.

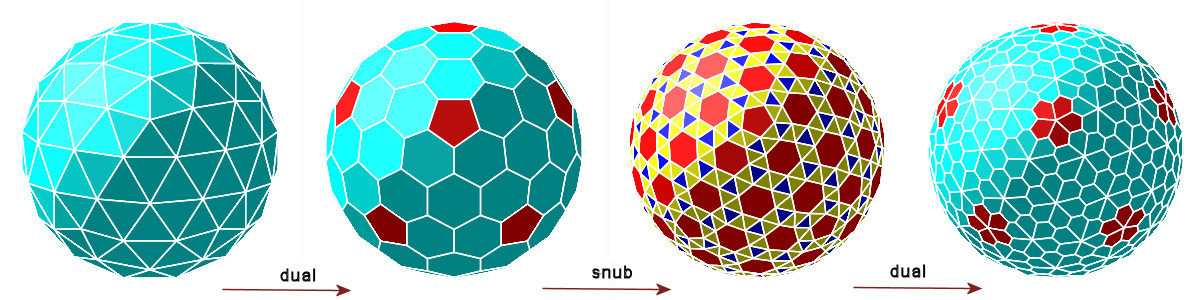
géode : 80 faces triangulaires dualGéode : 12 faces pentagonales, 60 faces hexagonales snubGéode : 362 faces dont 12 pentagones, 60 hexagones, 320 triangles géodeFleurs : 12 fleurs à 5 pétales, 20 fleurs à 6 pétales

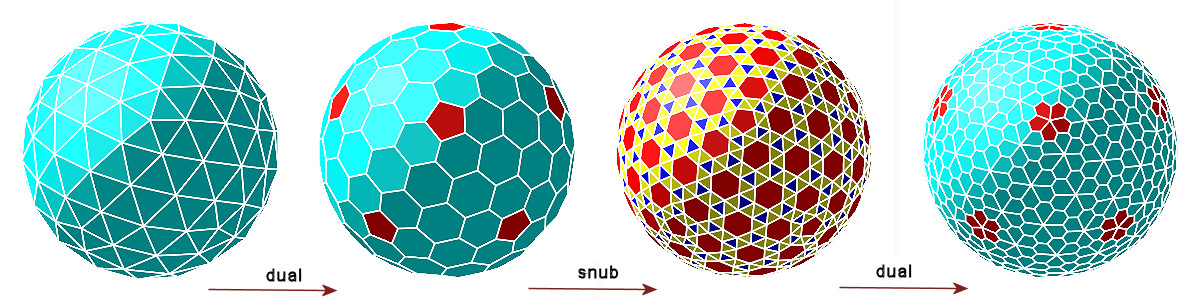
géode : 180 faces triangulaires dualGéode : 12 faces pentagonales, 80 faces hexagonales snubGéode : 812 faces dont 12 pentagones, 80 hexagones, 720 triangles géodeFleurs : 12 fleurs à 5 pétales, 80 fleurs à 6 pétales

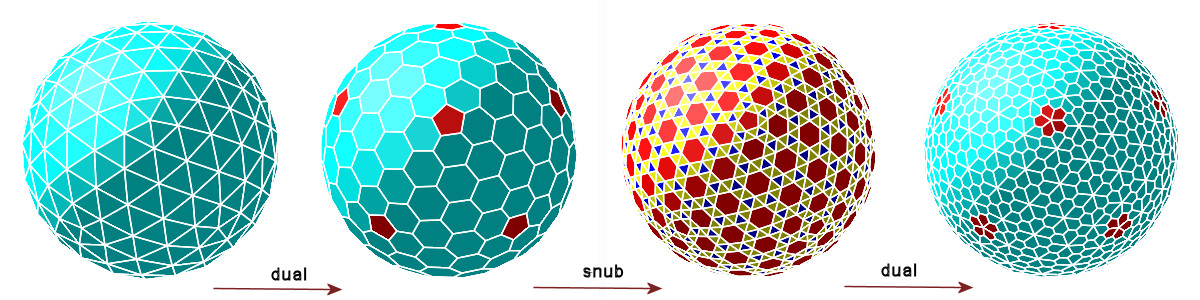
géode : 260 faces triangulaires dualGéode : 12 faces pentagonales, 120 faces hexagonales snubGéode : 1172 faces dont 12 pentagones, 120 hexagones, 1040 triangles géodeFleurs : 12 fleurs à 5 pétales, 120 fleurs à 6 pétales

géode : 380 faces triangulaires dualGéode : 12 faces pentagonales, 180 faces hexagonales snubGéode : 1712 faces dont 12 pentagones, 180 hexagones, 1520 triangles géodeFleurs : 12 fleurs à 5 pétales, 180 fleurs à 6 pétales

géode : 1040 faces triangulaires dualGéode : 12 faces pentagonales, 510 faces hexagonales snubGéode : 4682 faces dont 12 pentagones, 510 hexagones, 5120 triangles géodeFleurs : 12 fleurs à 5 pétales, 510 fleurs à 6 pétales