Expansion de polyèdres à faces triangulaires
Expansion pyramidale de polyèdres


anaglyphes en relief à regarder avec des lunettes rouge-cyan
Partie 1 : expansion par facettage des faces
On se propose de construire sur chaque face d'un polyèdre classique (P) à faces triangulaires trois facettes planes en forme de cerf-volant ; le polyèdre ainsi obtenu sera nommé expansion de (P) dans la suite de cette page.
Soit (A1, A2, A3) une face de (P) et O son centre.
Les milieux des cotés sont notés M12, M23, M31 ; leur distance à O sont notées respectivement l3, l1, l2.
K étant un coefficient et M l'équibarycentre de (M12, M23, M31), on détermine la fonction f du point G(K)=f(K)OM tel que les facettes (A1,M12,G,M31) ...etc, par permutation circulaire, soient planes.
Les coordonnées des points Ai sont notées [ai,bi,ci] pour i variant de 1 à 3.
Les coordonnées, en fonction de K et des {ai,bi,ci}, des trois facettes sont données dans ce fichier
En appliquant cette fonction aux différentes faces d'un polyèdre, on obtient la liste des faces de son expansion en fonction de K.
| 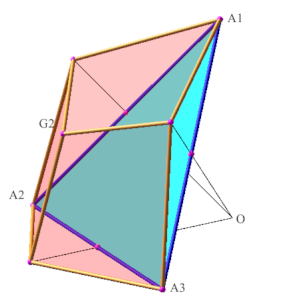
image des facettes pour K0 |
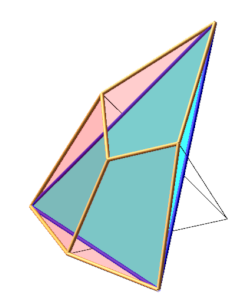
animation : souris sur image
|
Les paragraphes suivants en sont l'application aux faces de quelques polyèdres classiques.
I. Application : tétraèdre
Le fichier des coordonnées du tétraèdre et de son expansion sont dans ce fichier
| 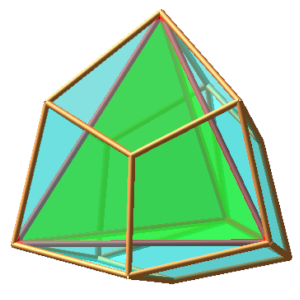
un exemple
|

animation : souris sur image
|
On passe du tétraèdre à un tétraèdre homothétique de rapport 3/2 en passant par un rhomboèdre à 12 faces.
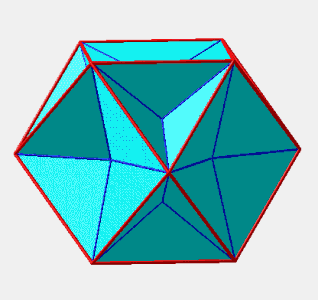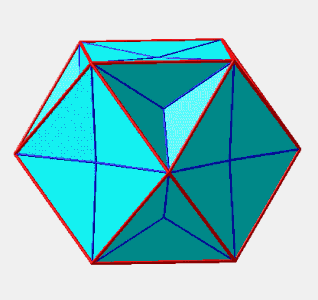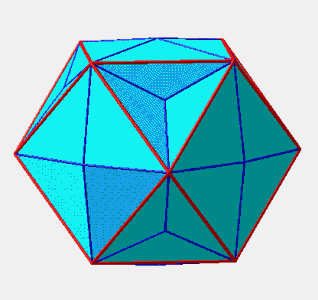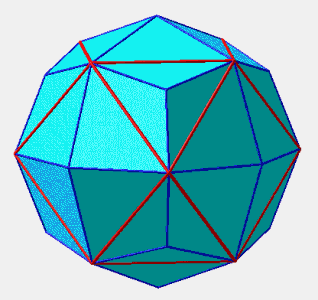
II. Application : octaèdre
Le fichier des coordonnées de l'octaèdre et de son expansion sont dans ce fichier
| 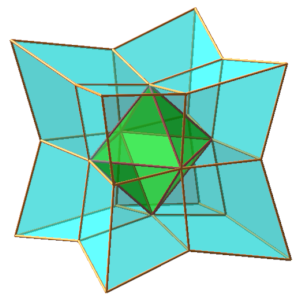
un exemple
|

animation : souris sur image
|
On passe de l'octaèdre à un cube en passant par un dodécaèdre rhombique.
III. Application : icosaèdre
Le fichier des coordonnées de l'icosaèdre et de son expansion sont dans ce fichier
| 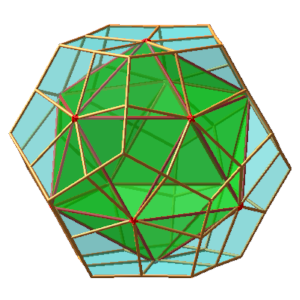
un exemple
|

animation : souris sur image
|
On passe de l'icosèdre à un dodécaèdre en passant par un hexacontaèdre semi-régulier.
Pour K=2, on obtient l'hexacontaèdre rhombique, solide à 60 faces constituées de losanges égaux.

IV. Application : cube étoilé
Le fichier des coordonnées du cube étoilé et de son expansion sont dans ce fichier
| 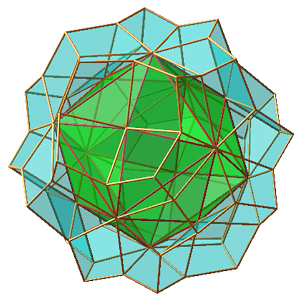
un exemple
|

animation : souris sur image
|
On passe du cube étoilé au polyèdre 
V. Application : triaki-tétraèdre
Le fichier des coordonnées du triaki-tétraèdre et de son expansion sont dans ce fichier
| 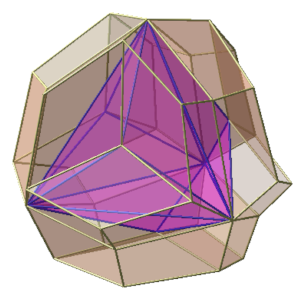
un exemple
|
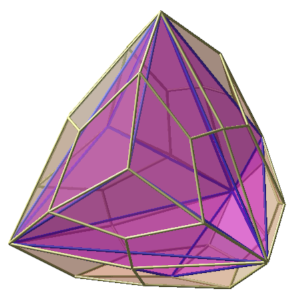
animation : souris sur image
|
On passe du triaki-tétraèdre au polyèdre 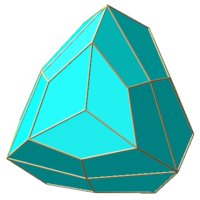
Partie 2 : expansion par augmentation des faces
On construit une pyramide régulière de hauteur h sur chaque face d'un polynôme régulier à faces triangulaires.
On passe par divers polyèdres intermédiaires(faces équilatérales, etc...).
Pour un polyèdre régulier, on a le cas particulier tel que les faces contigües de deux pyramides voisines soient coplanaires et forment alors un losange.