Familles de cercles tangents à trois cercles tangents deux à deux

Sur des sujets voisins, voir les pages :

empilements apolloniens
badernes spheriques
cercles-sphères Apollonius

Dans toute la suite, C1 désigne un cercle de rayon 1.
On part avec 3 cercles C1, C2, C3 ; C2 et C3 sont tangents extérieurement entre eux et tangents intérieurement à C1.

On cherche les cercles tangents simultanément, extérieurement à C2 et C3 et intérieurement à C1 : opération de ( type 1 )
Soit C4 une telle solution.
On réitère l'opération( type 1 ) avec { C1, C2, C4 } et { C1, C3, C4 }.
On cherche les cercles tangents simultanément, extérieurement à { C2, C3, C4 } : opération de ( type 2 ).

Et on continue avec les nouveaux triplets obtenus avec les opérations de type adéquat.

J'ai représenté soit les cercles soit les sphères ayant ces cercles pour cercle équatorial pour le coté esthétique.

Passer la souris sur les différentes images ...

triplet initial : deux cercles tangents de rayon 1/2 et tangents intérieurement à C1

triplet initial : trois cercles égaux tangents 2 à 2 et tangents intérieurement à C1

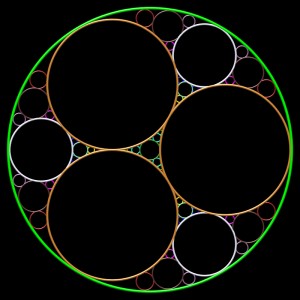
triplet initial : quatre cercles égaux tangents 2 à 2 et tangents intérieurement à C1

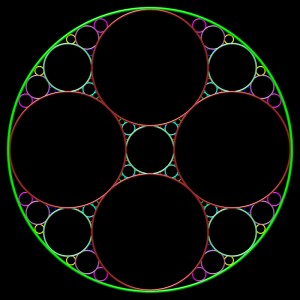
triplet initial : cinq cercles égaux tangents 2 à 2 et tangents intérieurement à C1

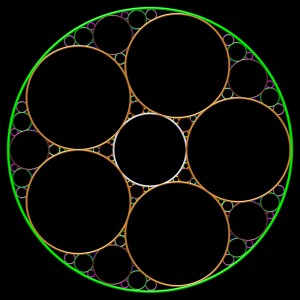
triplet initial : six cercles égaux tangents 2 à 2 et tangents intérieurement à C1

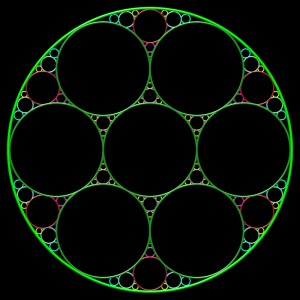
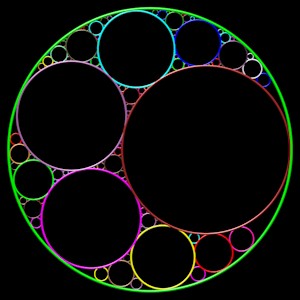
triplet initial : deux cercles inégaux tangents et tangents intérieurement à C1

triplet initial : trois cercles dont deux égaux tangents deux à deux et tangents intérieurement à C1

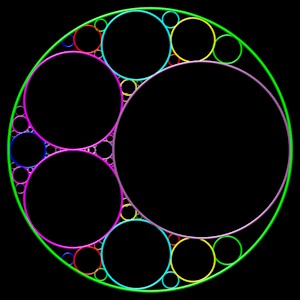
triplet initial : trois cercles inégaux tangents deux à deux et tangents intérieurement à C1

---

---

Début