Robert Ferréol m'a demandé s'il était possible de déterminer la structure géométrique des parties de paraboloïdes hyperboliques de la sculpture de Angel DUARTE, réalisée en 1973 et qui se trouve au bord du lac Léman à Ouchy-Lausanne.
En voici une photographie :

Pour toute la suite, les calculs ont été réalisés avec Maple et les résultats utilisés dans PovRay.
Les programmes Maple sont téléchargeables "zippés" : cliquer ici
La stucture de base est constituée de 8 triangles tracés sur les diagonales du polyèdre constitué de 7 cubes d'après le dessin ci-dessous.
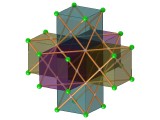
voir en 800x600
Chacun des quadrilatères gauches ainsi constitués par tous ces triangles, sert de base à une partie de paraboloîde engendré par des tiges s'appuyant sur deux cotés opposés d'un tel quadrilatère. On constate qu'il y a deux types de quadrilatères.
On peut considérer que la sculpture est une approximation de la réunion de six hyperboloïdes de révolution par les parties de paraboloïdes ci-dessus.
Voici ces six hyperboloïdes avec les 8 triangles qui en constituent des génératrices.
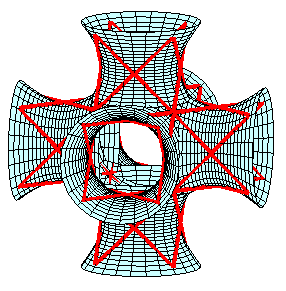
La deuxième partie très succinte du programme Maple construit les parties de paraboloïde dans deux quadrilatères contigus puis par des rotations successives, la sculpture complète.
Le programme PovRay traçant les images ci-dessous est téléchargeable : cliquer ici