Habillage polygonal d'une courbe fermée avec un ou des rubans continus
et rotoïdes à section polygonale
I. Principes de construction
Soit une courbe fermée d'équation OM(t) qui se referme pour la période P.
Je considère le repère (R) orthonormé lié au point courant M(t) : R = {T, U, V } constitué du vecteur T tangent à la courbe, du vecteur U perpendiculaire au plan {T, [0,0,1]} et V complétant ce repère et le repère (R1) R1 = {T,U1,V1} avec U1 et V1 déduits de U et V par une rotation d'axe T d'angle a0+a*t/P
La bande paramétrée B1(t,w) = OM(t)+k.U1+w.V1 est donc obtenue en "tordant" la bande paramétrée B(t,w) = OM(t)+k.U+w.V d'un angle a sur une période.
Avec n entier, a=2pi/n et a0 multiple de a, en répétant l'opération, on peut ainsi reboucler ces bandes les unes à la suite des autres donnant un habillage de la courbe.
On peut "tordre" de a ou 2a ... etc on obtient selon les cas un habillage avec un seul ruban continu ou deux rubans rubans continus alternés ...etc
Le trièdre de Serret-Frênet ne donne pas de résultats satisfaisants dans certains cas.
Le fichier PovRay réalisant les images ci-dessous est téléchargeable : Cliquer ICI
Quelques exemples :
| Tore : habillage à section carrée |
| tore - de 1 en 1 - 1 ruban
 |
tore - de 2 en 2 - 2 rubans
 |
tore - de 3 en 3 - 1 ruban
 |
| tore - de 1 en 1 - 1 ruban
 |
tore - de 2 en 2 - 2 rubans
 |
tore - de 3 en 3 - 1 ruban
 |
|
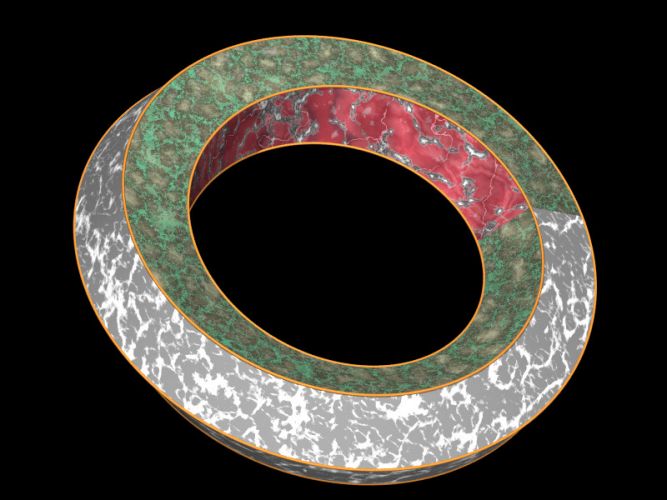
Tore : habillage à section pentagonale
|
|
tore - de 1 en 1
 |
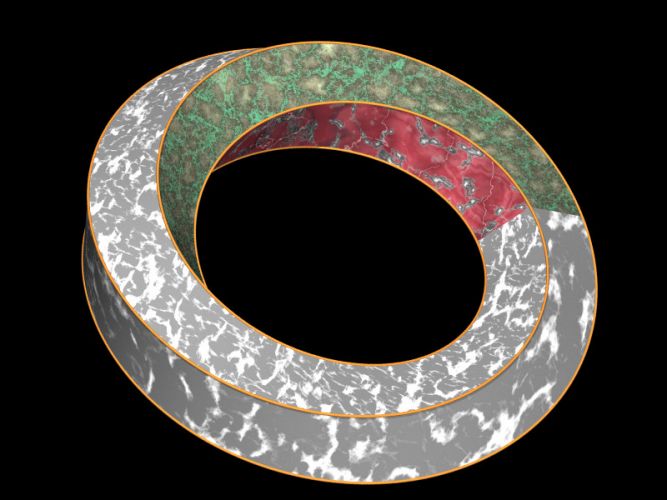
tore - de 2 en 2
 |
tore - de 3 en 3
 |
|
tore - de 1 en 1 - disjointes
 |
tore - de 2 en 2 - disjointes
 |
tore - de 3 en 3 - disjointes
 |
|
Noeud de trèfle
|
|
 |
 |
 |
|
sections hexagonale et octogonale croisées
|
|
 |
 |
II. Habillage lisse de section une courbe plane ( ici une ellipse )
Le fichier PovRay réalisant les images ci-dessous est téléchargeable : Cliquer ICI
|
habillage elliptique d'un nœud de trèfle
|
| habillage
 |
courbes coordonnées de l'habillage
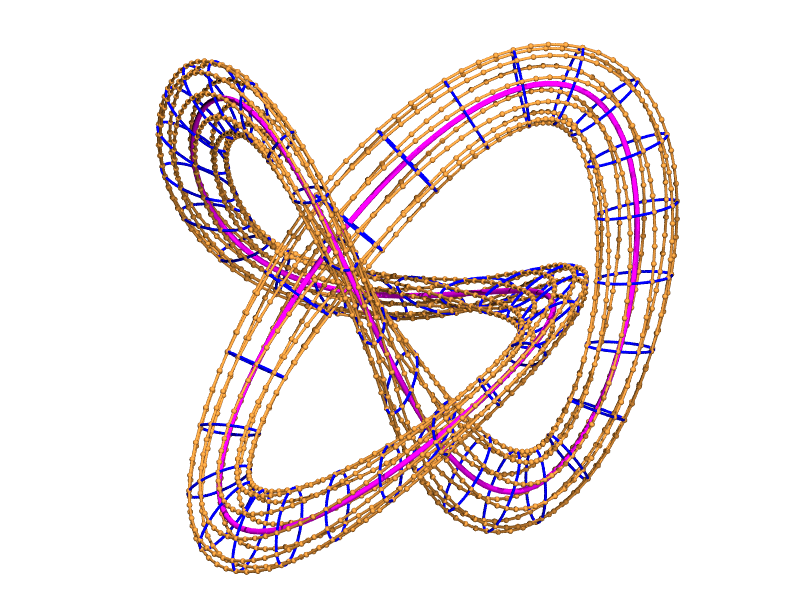 |
habillage + courbes coordonnées de l'habillage
 |
|
habillage elliptique d'un tore déformé
|
| habillage
 |
courbes coordonnées de l'habillage
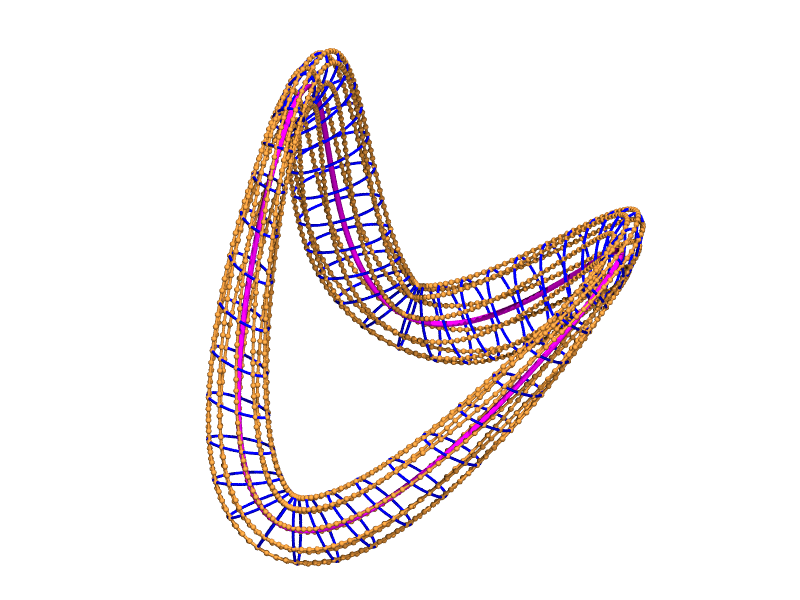 |
habillage + courbes coordonnées de l'habillage
 |
|
habillage elliptique d'un nœud torique
|
| habillage
 |
courbes coordonnées de l'habillage
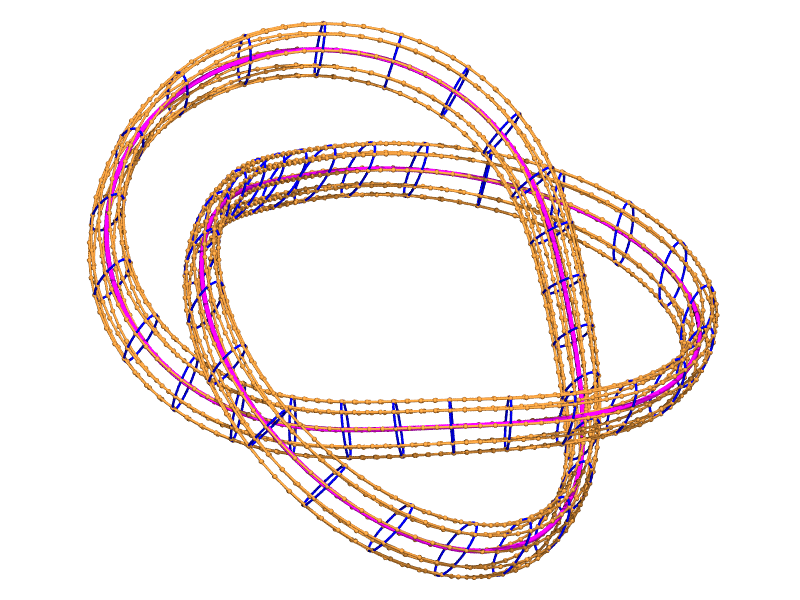 |
habillage + courbes coordonnées de l'habillage
 |

























