Fractals à partir de polyèdres
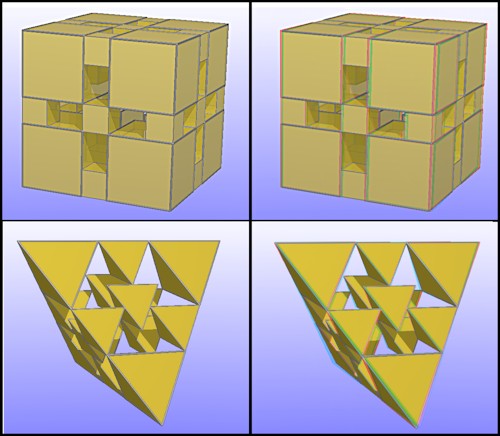
Les images ont été fabriquées avec le logiciel PovRay. Ces objets sont difficiles à interpréter sur une image plate car les traits se mélangent, la vision stéréoscopique permet une bien meilleure compréhension des formes obtenues.
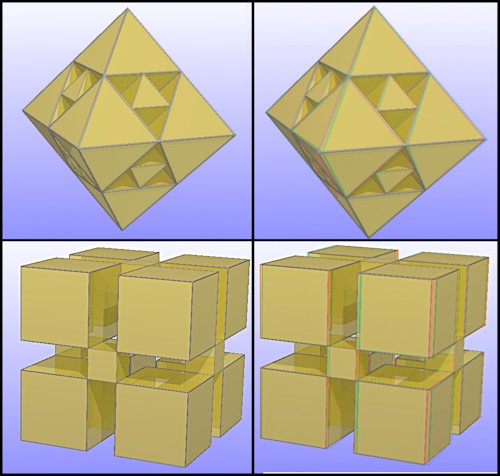
Les images de droite sont des anaglyphes à regarder avec des lunettes rouge-cyan.
Première méthode de construction
On fait subir à un polyèdre P0 des homothéties de centres les sommets et de rapport k : on obtient ainsi un polyèdre P1 plus ou moins creux constitué de petits polyèdres semblables à P0 ; on réitère le procédé sur P1 pour obtenir l'itéré P2 ... etc.
Une arête AB de P0 est remplacée par les deux arêtes homologues AB' et A'B dans les homothéties ayant pour centres les sommets A et B. Si k est supérieur à 1/2, il y a chevauchement et l'objet obtenu peu intéressant visuellement.
Pour k = 1/2 : P0 parallélépipède est sans intérêt car globalement Pn est identique à P0 ; si P0 est un tétraèdre, on obtient le tétraèdre de Sierpinski.
Cliquer pour avoir l'Animation des itérés successifs en 2D et 3D

Deuxième méthode de construction
On fait subir à un polyèdre P0 des homothéties de centres les sommets de rapport k et des homothéties de centres les milieux des cotés de rapport k1 : on obtient ainsi un polyèdre P1 plus ou moins creux constitué de petits polyèdres semblables à P0 ; on réitère le procédé sur P1 pour obtenir l'itéré P2 ... etc.
Une arête AB de milieu M de P0 est remplacée par les trois arêtes dans les homothéties ayant pour centres A, B et M.
Pour qu'il n'y ait paschevauchement de ces arêtes transformées, il faut que k < 1/2 et k1 <= 1-2k.
k = k1 = 1/3 : les trasformés par homothéties sont tous égaux
Si P0 est un parallélépipède, on obtient l'éponge de Menger ; on peut aussi partir d'un prisme, un tétraèdre un octaèdre ...etc
Cliquer pour avoir l'Animation des itérés successifs en 2D et 3D
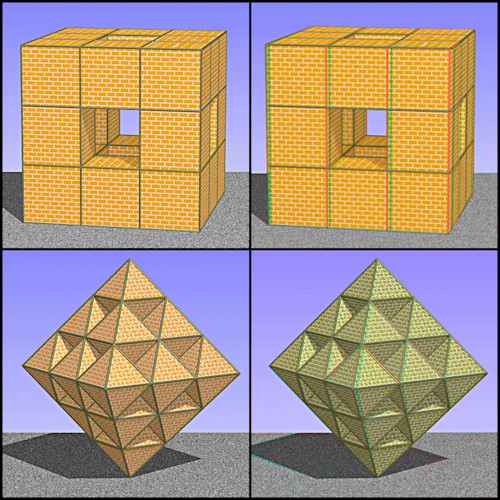
k < 1/2 et k1 = 1-2k : les trasformés par homothéties ne sont pas égaux
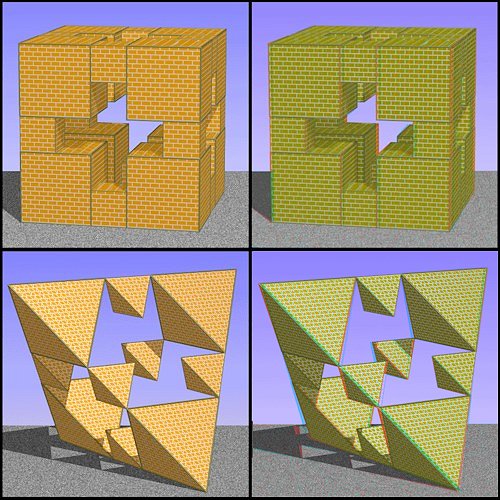
Si P0 est un parallélépipède, on obtient des trous en forme de croix ; on peut aussi partir d'un prisme, un tétraèdre un octaèdre ...etc
Pour k=4/10 et P0 un cube, on obtient une croix régulière ( croix suisse ).
Cliquer pour avoir l'Animation des itérés successifs en 2D et 3D
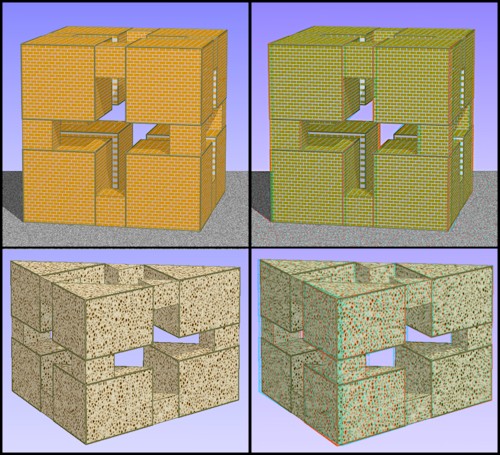
Troisième méthode de construction
On prend un cube P0 et P1=P0.
P2 est la réunion de :
des homothétiques de P1 de centres les sommets de rapport k.
des homothétiques de P0 de centres les milieux des arêtes de rapport k*k.
Si l'on prend k tel k*k=1-2*k soit k=sqrt(2)-1, alors sur une arête AB de P2, on trouve cote-à-cote cinq homothétiques de P0 de même taille.
Quatre proviennent des transformés de P1 et celui du milieu, du transformé de P0.
... et on itére le processus.
Cliquer pour avoir l'Animation des itérés successifs en 2D et 3D
Autres méthodes de construction
On peut refaire les diverses méthodes ci-dessus en remplaçant les milieux des arêtes par les milieux des faces ou en cumulant milieux des arêtes et des faces.
Sommets et milieux des faces
On prend un cube P0 et P1=P0.
P2 est la réunion de :
des homothétiques de P1 de centres les sommets de rapport k.
des homothétiques de P0 de centres les milieux des faces de rapport k*k.
Cliquer pour avoir l'Animation des itérés successifs en 2D et 3D
Sommets, milieux des arêtes et des faces
On prend un cube P0 et P1=P0.
P2 est la réunion de :
des homothétiques de P1 de centres les sommets de rapport k.
des homothétiques de P0 de centres les milieux des arêtes et des faces de rapport 1-2k.
Cliquer pour avoir l'Animation des itérés successifs en 2D et 3D