Télécharger : le fichier Maple "zippé
Polyèdres
I. Troncature d'un polyèdre
Ceci a été initié par Robert Ferréol ; pour de savantes et nombreuses précisions :
voir son site
Pour des représentations de polyèdres avec PovRay, voir ma page :
Polyèdres
Deux types de faces figurent dans le polyèdre tronqué :
celles correspondant à la partie résiduelle des faces initiales,
celles correspondant à la base des pyramides supprimées en tronquant les sommets.
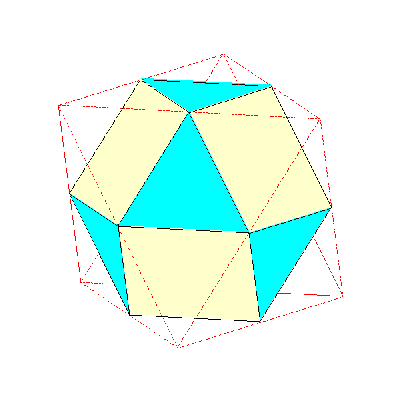
J'ai rencontré quelques difficultés pour obtenir et faire tracer ces dernières : je suis intéressé par tout algorithme plus adroit que ceux utilisés.
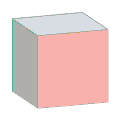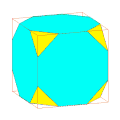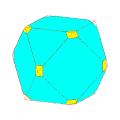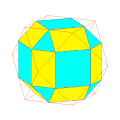
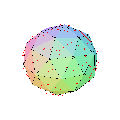
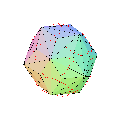
Pour un choix convenable du coefficient de troncature, les polyèdres réguliers donnent des polyèdres semi-réguliers :
Quelques exemples de troncatures de rapport variable en partant de :
Quelques exemples de troncatures successives de rapport 1/2 ou 1/3 en partant de :
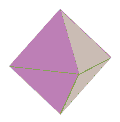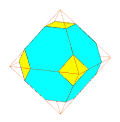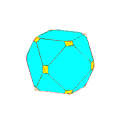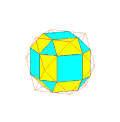
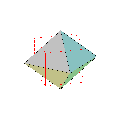
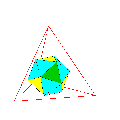
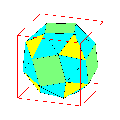
II. Dual d'un polyèdre
Soit (S) une sphère centrée au centre du polyèdre.
On appelle dual d'un polyèdre, le polyèdre dont chaque sommet est le dual par rapport à (S) de chaque face du polyèdre initial.
Pour les polyèdres de Platon, si l'on prend la sphère inscrite pour sphère (S), alors cette sphère est tangente aux faces en leur centre et le polyèdre dual a donc pour sommets les centres des faces, définition que l'on trouve sur de nombreux sites.
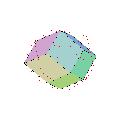
Quelques exemples, dans une colonne, on peut télecharger deux images en 600x600 représentant :
- un polyèdre et son dual,
- le dual et le dual du dual.
Pour chaque image :
- en mode fil de fer rouge : le polyèdre initial,
- en mode normal : le dual.
On constate que le dual du dual d'un polyèdre est ce même polyèdre.
Tracés avec le logiciel PovRay :
- le dual d'un "snub" icosaèdre
- le dual d'un pentakisdodécaèdre tronqué
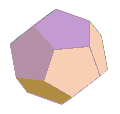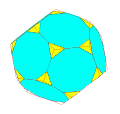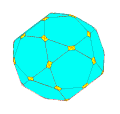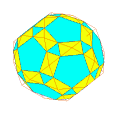
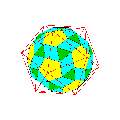
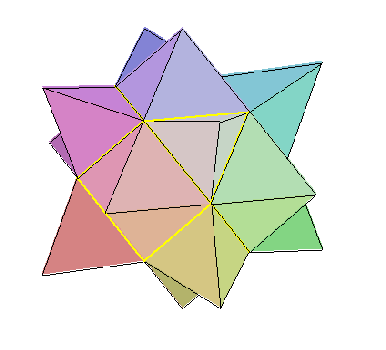
III. Polyèdres adoucis ou camus
Soit un polyèdre de l'ensemble {tétraèdre, cube, icosaèdre, dodécaèdre, ... }.

1. On fait subir à chaque face une similitude (S) de centre le centre de la face, de rapport k d'angle t : faces en vert,
2. Pour chaque sommet, les transformés par les similitudes (S) associées aux faces adjacentes à ce sommet, donnent une face : faces en jaune,
3. Pour chaque arête [A,B], soient [A1,B1], [A2,B2], les transformés par les similitudes (S) associées aux deux faces adjacentes ; on construit les faces triangulaires [A1,B1,A2], [A2,B2,B1]: faces en bleu.
Si l'angle t est nul, alors les deux triangles [A1,B1,A2], [A2,B2,B1] sont coplanaires et forment un parallélogramme, ce qui revient à chanfreiner l'arête.
Le polyèdre ainsi obtenu avec ces différentes faces est appelé une forme adoucie du polyèdre initial.
Si on détermine k et t pour que le triangle [A1,B1,A2] soit équilatéral, le polyèdre adouci est le "snub" polyèdre ou polydre camus associé .
Si l'on prend l'angle t nul, la similitude se réduit à une homothétie et les deux triangles [A1,B1,A2], [A2,B2,B1] forment un rectangle ce qui revient à chanfreiner les arêtes ; je dirai que le polyèdre obtenu est le polyèdre initial chanfreiné.
On remarque que le tétraèdre adouci est un icosaèdre inscrit dans le tétraèdre.
La chiralité du subcube ou snubdodécaèdre est la propriété d'avoir deux représentants symètriques par rapport à un plan et non superposables ; l'un est l'image de l'autre dans un miroir.
Une animation et quelques autres images de polyèdres adoucis à partir de :
prisme pentagonal
icosaèdre tronqué
octaèdre tronqué
Petit rhombicuboctaèdre
chanfreinage : animation
Tracés avec le logiciel PovRay :
- un "snub" icosaèdre
- un "snub" pentagonalicositetraèdre
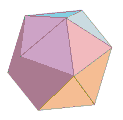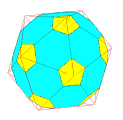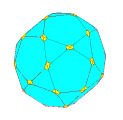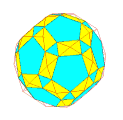
Remarque : En chanfreinant tétraèdre, cube, octaèdre, icosaèdre et dodécaèdre avec des coefficients convenables on peut obtenir certains des polyèdres semi-réguliers ; ci-dessous, un tabeau de ces résultats :
tétraèdre ->
cuboctaèdre
coefficient = 1/4
voir
| Cube ->
petit rhombicuboctaèdre
coefficient = 2^(1/2)-1
voir
|
octaèdre ->
petit rhombicuboctaèdre
coefficient = (-2+3*2^(1/2))/7
voir
|
icosaèdre ->
petit rhombicosidodécactaèdre
coefficient = (3*5^(1/2)+1)/22
voir
|
dodécaèdre ->
petit rhombicosidodécactaèdre
coefficient = (1+5^(1/2))/6
voir
|
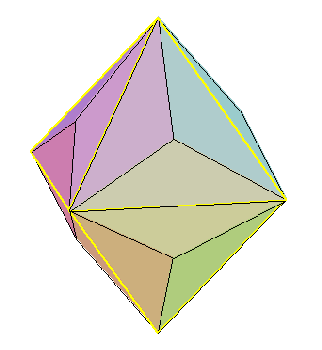
IV. Augmentation "pyramidale" d'un polyèdre
Cette transformation est à appliquer à un polyèdre n'ayant pour faces que des polygones réguliers.
On remplace chaque face par la pyramide régulière constituée de triangles isocèles et dont le sommet est à l'extérieur du polyèdre ( exemple 1 : triangles isocèles ; exemple 2 : triangles équilatéraux ) ou à l'intérieur ( exemple 3 )
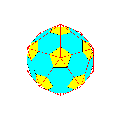
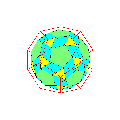
V. Géode
Ceci a été initié par un article de Gérard Lavau dans la revue de l'UPS.
Les faces triangulaires d'une géode initiale( icosaèdre, octaèdre ) étaient subdivisées par des parallèles aux cotés en triangles égaux qui étaient ensuite projetés sur la sphère circonscrite donnant ainsi naissance à une nouvelle géode.
Partant d'un polyèdre quelconque inscrit dans la sphère (S) de rayon 1, j'ai projeté les milieux des arêtes sur la sphère (S).
J'ai considéré pour chaque face :
les triangles obtenus avec un sommet et les projetés des milieux des deux arêtes adjacentes,
le polygone construit avec les projetés des milieux des arêtes ;
On obtient ainsi une nouvelle géode et l'on peut réitérer le processus.
Si la face initiale de la géode n'est pas un polygone régulier, la partie centrale de la transformée n'est pas forcément plane ; si toutes les faces sont des polygones réguliers ou des triangles, les géodes itérées sont à faces planes.
On obtient ainsi des structures ayant un aspect remarquable.

 Début
Début







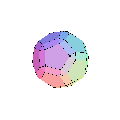








 Début
Début