Pavages hyperboliques

I. Principes

On appelle :
      segment hyperbolique , un arc d'un cercle orthogonal à (DP), arc contenu dans le disque unité (DP) et d'extrémités A et B,
      polygone hyperbolique , un polygone curviligne dont les cotés sont des segments hyperboliques.

On considère les sommets d'un polygone régulier de centre O, à n cotés, de cercle circonscrit le cercle de rayon r < 1 et le polygone hyperbolique (P0) ayant les mêmes sommets.
Les angles de (P0) varient selon la valeur de r.
On veut calculer r de telle façon que si l'on réitère les symétries hyperboliques par rapport aux cotés de P0, on obtienne exactement k polygones hyperboliques contigus autour de chaque sommet de (P0) ( et également pour les symétriques ).
Comme conséquence des symétries hyperboliques, k fois l'angle au sommet du polygone hyperbolique vaut donc 2*pi.

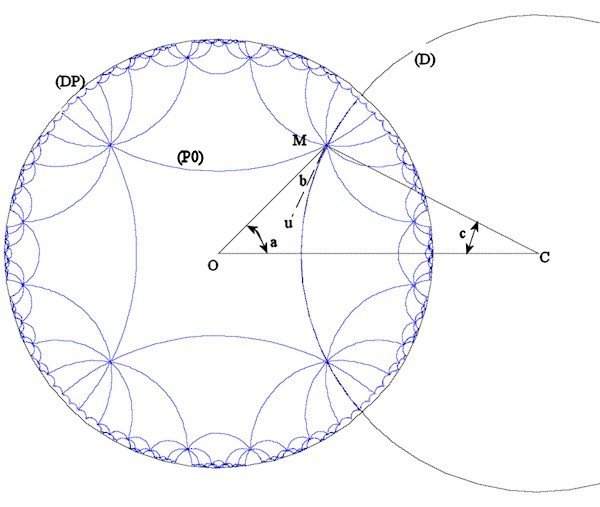
Pavage avec n = 4 et k = 10 nommé "pavage hyperbolique (4,10)" Mu étant la tangente à (D), le demi-angle au sommet, b, du polygone hyperbolique vaut pi/k. L'angle a vaut pi/n et par suite c = pi/2 -a-b. En utilisant la relation : MC/sin(a) = OC/sin(Pi/2+b) = OM/ sin(c), on peut calculer OM = r en fonction de n et k. On trouve aisément : r = sqrt(2/(cos(2*Pi/n)+cos(2*Pi/k)))*cos((Pi/k+Pi/n));

Algorithme utilisé :
Je calcule à l'aide d'une boucle les images des extrémités des cotés des polygones hyperboliques par les symétries hyperboliques SH(i) par rapport aux segments hyperboliques constituant les cotés du polygone hyperbolique (P0) initial, régulier, de centre O à n cotés.

1. On initialise les listes L(i) avec le couple (m(i),m((i mod n)+1)) des extrémités du coté c(i) de (P0) ( + éventuellement rayons, "médianes" ) pour i variant de 1 à n.
2. A l'étape k, on calcule les images par les SH(i) des couples des L(j) pour j différent de i, images que l'on met dans L(j) après sauvegarde du contenu pour le résultat final.
3. Le résultat final obtenu, on calcule une réprésention paramétrique des lignes hyperboliques d'extrémités les couples obtenus.

J'utilise le même principe pour les surfaces : calcul des sommets des triangles curvilignes puis coloriage des triangles curvilignes.

Les programmes ont été réalisés avec Maple ; l'exécution est rapide si on se limite aux courbes seules, beaucoup plus lente pour les surfaces coloriées.

II. Exemples

On obtient des figures assez dissemblables selon :
     les valeurs différentes de n et k,
     au départ seulement le polynôme (P0),
     au départ le polynôme (P0) et ses rayons,
     au départ le polynôme (P0) et ses rayons et les segments joignant le centre aux milieux de ses cotés.

Je peux envoyer le programme si quelqu'un est intéressé.

pavage hyperbolique(3-8)	pavage hyperbolique(3-8) + rayons	pavage hyperbolique(3-12) + rayons + "médianes"
pavage hyperbolique(4-6)	pavage hyperbolique((4-6) + rayons	pavage hyperbolique(4-6) + rayons + "médianes"
pavage hyperbolique(6-4)	pavage hyperbolique(6-4) + rayons	pavage hyperbolique(6-4) + rayons + "médianes"
pavage hyperbolique(5-4) avec rayons	pavage hyperbolique(8-4) avec "médianes"	pavage hyperbolique(3-12)

On peut partir d'un pavé hyperbolique régulier non centré à l'origine ce qui donne un pavage qui ne possède plus les mêmes symétries euclidiennes.

pavage hyperbolique(4-6) décalé	pavage hyperbolique(4-6) décalé avec rayons
pavage hyperbolique(6-4) décalé	pavage hyperbolique(8-3) décalé+rayons+médianes

Avec le logiciel PovRay : ce que l'on verrait dans une chambre hyperbolique dont les six murs sont des glaces.
( voir : http://images.math.cnrs.fr/Une-chambre-hyperbolique.html )


L'anglyphe à regarder avec des lunettes rouge-cyan :