télécharger le fichier Maple "zippé"
Courbes de Koch et variantes
I. Construction classique
L'itéré d'orde n, (n>1) de la courbe de Koch peut s'obtenir en remplaçant chaque segment AB de l'itéré d'ordre (n-1) par le motif ACDEB ci-dessous où le triangle CDE est équilatéral.
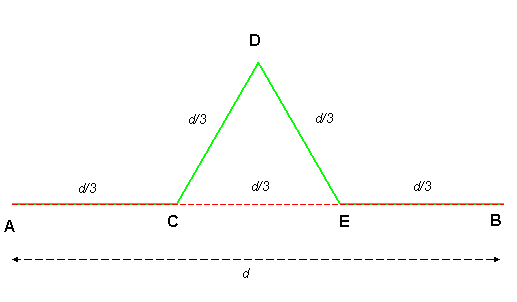
Si l'on prend pour comme ligne de départ (itéré d'orde 1) un segment, on obtient la Courbe de Koch classique :

Si l'on prend pour comme ligne de départ (itéré d'orde 1) un triangle équilatéral, on obtient le flocon de Koch classique :

On peut changer de motif et/ou de ligne brisée de départ :
départ : un carré, même motif que ci-dessus : voir l'animation
départ : un triangle, motif ci-dessus inversé : voir l'animation
départ : un carré, motif avec triangle rectangle isocèle : voir l'animation
départ : une ligne brisée, motif avec triangle équilatéral inversé : voir l'animation
départ : un carré, motif avec triangle isocèle : voir l'animation
départ : un pentagone, motif "quelconque" : voir l'animation
II. Construction par rotation d'un polygone
Une autre façon d'obtenir ces courbes dans le cas d'un motif formé de quatre segments égaux dont les deux intermédiaires peuvent être considérés comme deux cotés adjacents d'un polygone régulier Pn à n cotés est la suivante :
On considère un polygone semblable à Pn construit sur chaque segment AB d'un itéré et on le fait tourner de Pi/n autour de son centre ; ce polygone crée un triangle CDE sur AB, la ligne brisée ACDEB remplace AB dans le nouvel itéré.
départ : un segment AB ; polygone : un triangle équilatéral.
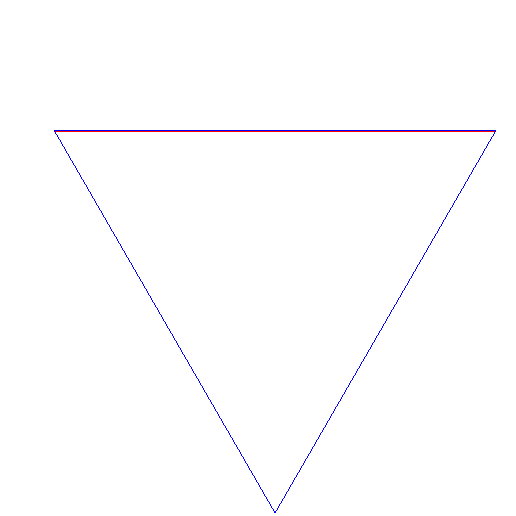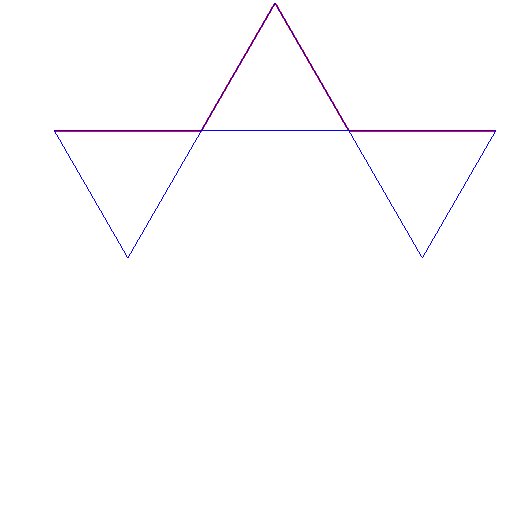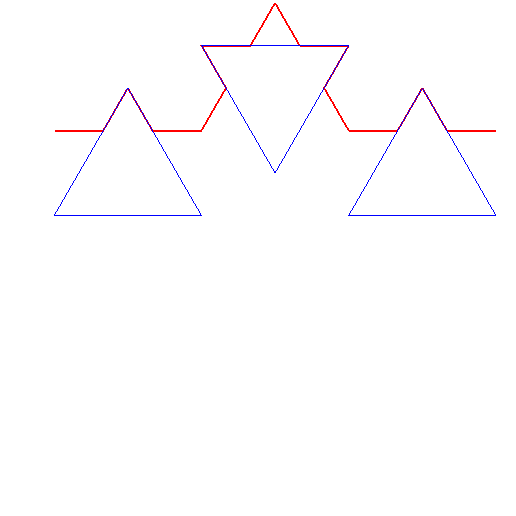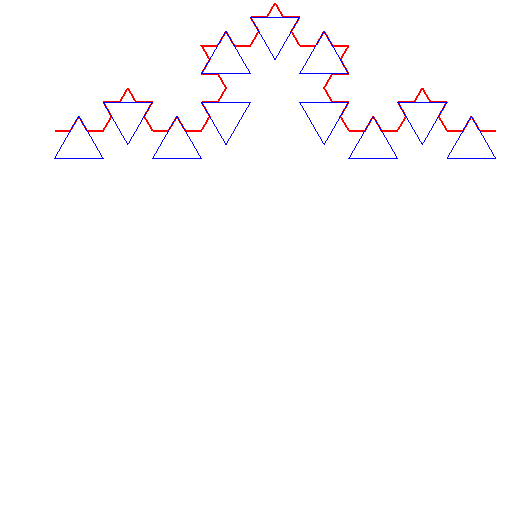
départ : un segment AB ; polygone : un carré : voir l'animation
départ : un triangle équilatéral ; polygone : un triangle équilatéral : voir l'animation
départ : un carré ; polygone : un triangle équilatéral : voir l'animation
départ : un carré ; polygone : un carré : voir l'animation
départ : un carré ; polygone : un carré inversé : voir l'animation
départ : un carré ; polygone : un triangle équilatéral inversé : voir l'animation
départ : un pentagone régulier ; polygone : un pentagone régulier : voir l'animation
départ : un polygone quelconque ; polygone : un carré : voir l'animation

 Début
Début





 Début
Début