Soit un polyèdre (P) convexe donné par la liste de ses n faces Lfaces = [face[1], face[2].., face[n]].
Une face est donnée par la liste de ses p sommets contigüs face[i] = [sommet[1],.., sommet[p]].
L'équation eq[i](M)=0 du plan de face[i] est de la forme f(x,y,z) = ax+by+cz-d avec M(x,y,z).
eq[i](M) change de signe quand M traverse le plan de face[i].
Soit G l'équibarycentre des sommets de (P) ; G intérieur à (P) puisque convexe.
Soit sign(eq[i](G)) = -1 si eq[i](G) < 0 sinon +1 .
Pour tout i, l'expression EQ[i](M) = eq[i](M) * sign(eq[i](G)) est positive ou nulle pour M situé dans le demi_espace limité par le plan d'équation eq[i](M)=0 et contenant le barycentre G .
La fonction notée min(x1,x2 ,..,xn) donne le minimum de ces nombres.(* voir son expression avec la valeur absolue en fin de page)
Soit EQP(M) = min( EQ[1](M), EQ[2](M),..,EQ[n](M) ).
EQP(M) = 0 est donc vérifiée si M est situé dans l'intersection des demi-espaces précédents et au moins sur un des plans contenant une face.
EQP(M) = 0 est donc l'équation cartésienne implicite de la réunion des faces du polyèdre convexe (P).
Exemple : icosidodécaèdre
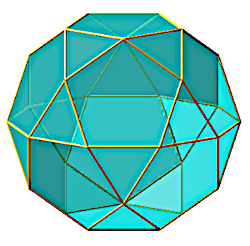Ici le programme Maple succint
II. Polyèdre non convexe
Soit un polyèdre(P) non convexe que l'on suppose décomposé en une réunion de n polyèdres p[j] convexes dont on a établi les équations cartésiennes selon le paragraphe précédent.
Soit EQp[j](M) = 0, j=1..p,ces équations et EQ(M) = max( EQp[1](M),EQp[2](M),..,EQp[n](M) ).
EQ(M) = 0 alors EQp[j](M) <=0 pour tout j et il existe au moins un j tel que EQp[j](M)=0
donc M appartient au moins à un (p[j])
EQ(M) = 0 est donc l'équation cartésienne implicite de la réunion des faces des polyèdres p[j])
Remarque : Les faces cachées des polyèdres intermédiaires utilisés sont invisibles dans la représentation graphique.
Exemple : dodécagone étoilé
Ici le programme Maple succint
III. Un exemple d'application de min
Soit (P) un polyèdre convexe à n faces, on se propose de trouver l'ensemble des points M tels que la projection orthogonale sur chaque face soit à l'intérieur de la face.
Pour chaque face[i] , on établit l'équation cartésienne EQ_plan[i,j] du plan contenant l'arête j et orthogonal à cette face(avec le "bon" signe : voir sign(eq[i](G) ci-dessus).
Soit Leq_plans:=[ [ EQ_plan[1,1], EQ_plan[1,2],..], [ EQ_plan[2,1], EQ_plan[2,2],..],... ,[ EQ_plan[n,1], EQ_plan[n,2],..] ]
L'équation implicite de l'ensemble cherché est
EQ := min( min( EQ_plan[1,1],EQ_plan[1,2],.. ), min( EQ_plan[2,1],EQ_plan[2,2],.. ),... , min( EQ_plan[n,1],EQ_plan[n,2],.. ) )
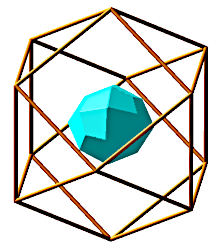Ici le programme Maple
IV. Généralistion : intersection(max), réunion et différence(min) de surfaces en implicite
Soient deux surfaces (S1) et (S2) d'équations implicites EQ1 et EQ2.
max(EQ1,EQ2) est l'équation implicite de leur intersection.
min(EQ1,EQ2) est l'équation implicite de leur réunion.
min(-EQ1,EQ2) est l'équation implicite de la différence.
Exemple : sphère et cylindre
Ici le programme Maple
(*)Expression de min(a1,a2,..,an) avec la fonction abs :
minabs(L) (* L est une liste de valeurs notée L[a1,a2,.. ,an] *)
n le nombre déléments de L
Si n est impair alors
si n=1
L[1]
sinon
u=L[1]: v=minabs(L[2..n]):
(u+v-abs(u-v))/2
sinon
u=minabs(L[1..n/2]: v=minabs(L[n/2+1..n]):
(u+v-abs(u-v))/2
Début