Voir : le fichier Maple "zippé"
ou bien: le fichier Maple version 18
Couture d'une balle de tennis
I. Couture modèlisée par une hypotrochoïde
Avec Robert Ferréol, nous avions déjà cherché diverses courbes mathématiques ayant quelques ressemblances avec la couture d'une balle de tennis.
Ultérieurement, nous avons étudié une courbe pouvant servir de modèle mathématique à un bijou sur la demande d'un bijoutier suisse.
voir la page correspondante de Robert Ferréol : ICI
Ayant fait le rapprochement de forme avec la couture de la balle, nous avons cherché les valeurs des paramètes des équations donnant la courbe la plus visuellement satisfaisante. Les équations paramétriques retenues pour la couture sont :
x = a*cos(t)+b*cos(3*t)
y = a*sin(t)-b*sin(3*t) avec b = a/3
z = 2*sqrt(a*b)*sin(2*t)
Balle de tennis virtuelle obtenue avec le logiciel PovRay et les équations ci-dessus

Ci-dessous, diverses formes de cette courbe et la courbe retenue sous divers angles.
II. Couture modèlisée par quatre arcs de cercles égaux qui se raccordent tangentiellement
Les équations paramétriques de ces quatre arcs de cercles sont :
R := 1: h := sqrt(R^2-r^2): r:=R*sqrt((1/2)*sin(theta)^2+1/2):
t0:= arctan((1/2)*sin(theta)*(4-2*cos(theta)^2)/(cos(theta)^2-2)):
cercle1 = [r*cos(t), h*cos(theta)-r*sin(theta)*sin(t), h*sin(theta)+r*cos(theta)*sin(t)] pour -t0 <= t <= Pi+t0
cercle2 = [r*cos(t), -h*cos(theta)+r*sin(theta)*sin(t), h*sin(theta)+r*cos(theta)*sin(t)] pour -t0 <= t <= Pi+t0
cercle3 = [-h*cos(theta)-r*sin(theta)*sin(t), r*cos(t), -h*sin(theta)+r*cos(theta)*sin(t)] pour -Pi-t0 <= t <= t0
cercle4 = [h*cos(theta)+r*sin(theta)*sin(t), r*cos(t), -h*sin(theta)+r*cos(theta)*sin(t)] pour -Pi-t0 <= t <= t0
Quelques positions des arcs de cercles avec leur axe :
En particulier pour theta=0, on obtient quatre demi-cercles dont les axes sont confondus 2 à 2 ( 3-ième de la ligne 1 ).
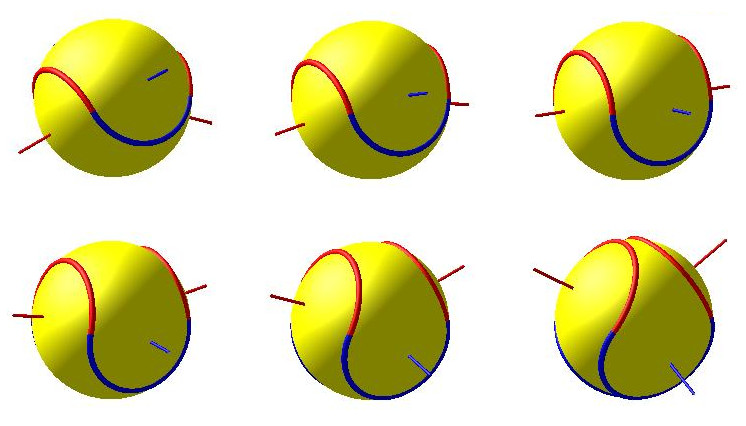
Animation
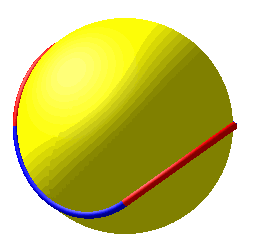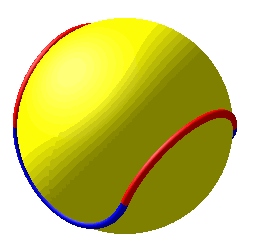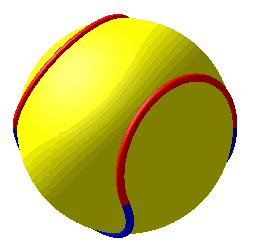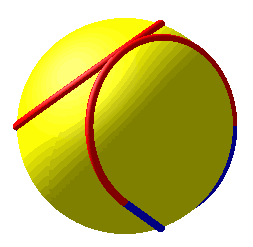
III. Couture modèlisée par la projection conique de quatre demi-ellipses
On considère quatre demi-ellipses placées comme ci-dessous et on considère leur projection conique, de sommet le centre de la sphère, sur la sphère.
Ci-dessous, diverses formes de la courbe projection et la courbe retenue sous divers angles.
IV. Couture modèlisée à partir d'équations de JB Roux
Les équations utilisées sont une variante d'équations trouvées sur un site de JB Roux
x = (a*cos(t+Pi/4)+b*cos(3*(t+Pi/4)))*(1-d*sin(2*t))/D:
y = (a*sin(t+Pi/4)-b*sin(3*(t+Pi/4)))*(1+d*sin(2*t))/D:
z = 2*sqrt(a*b)*sin(2*(t+Pi/4))/D:
où D = sqrt(x^2+y^2+z^2)):
Balle de tennis virtuelle obtenue avec le logiciel PovRay et les équations ci-dessus

Ci-dessous, diverses formes de la courbe projection et la courbe retenue sous divers angles.
Pour des précisions mathématiques, voir la page de Robert ferréol ICI
 Début
Début


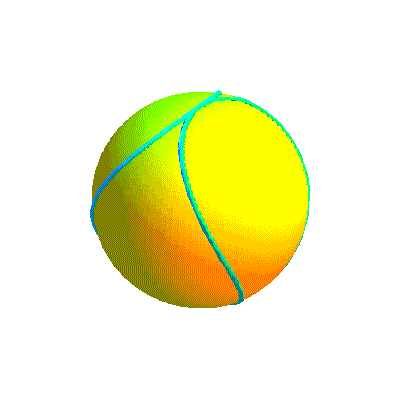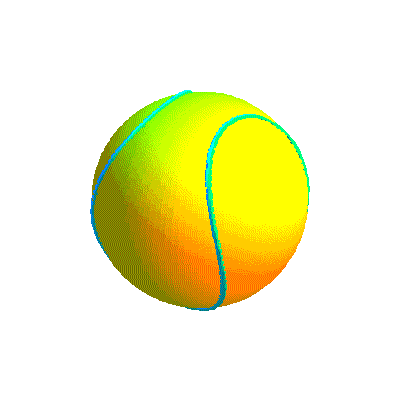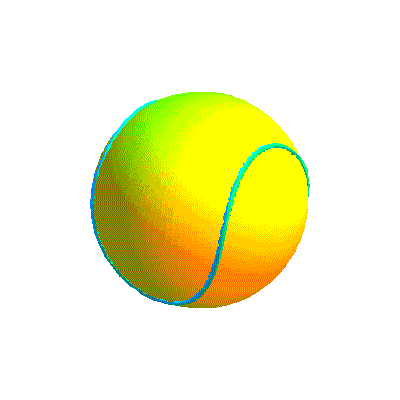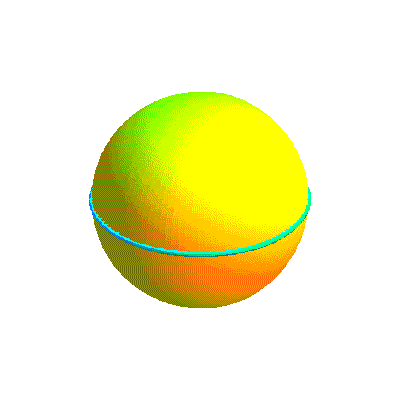
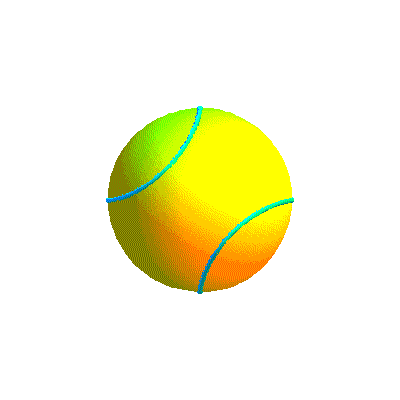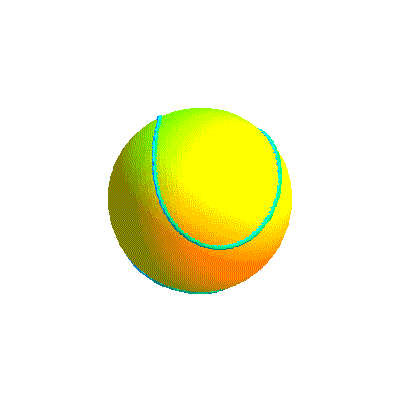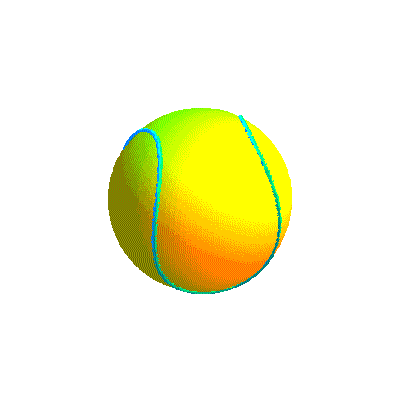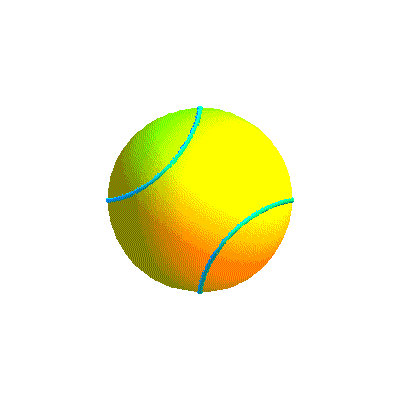


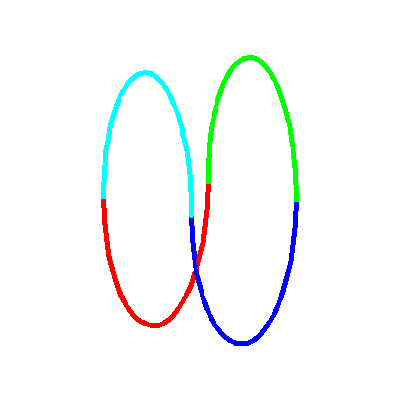
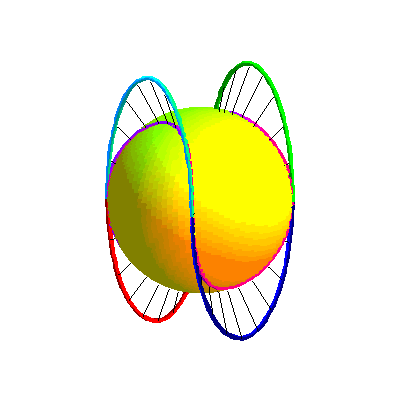
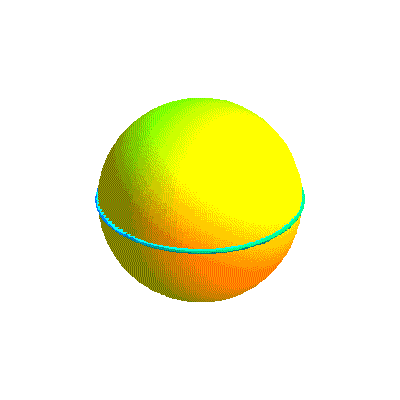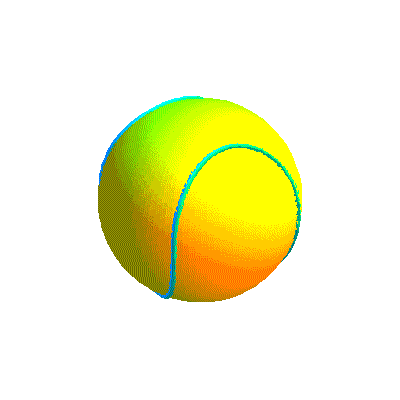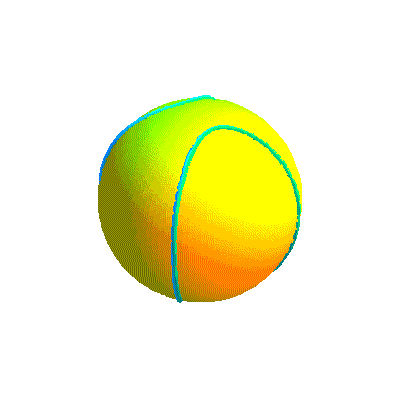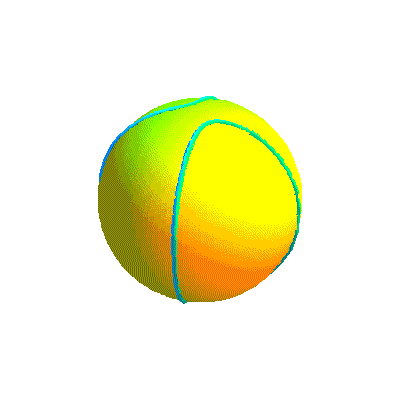
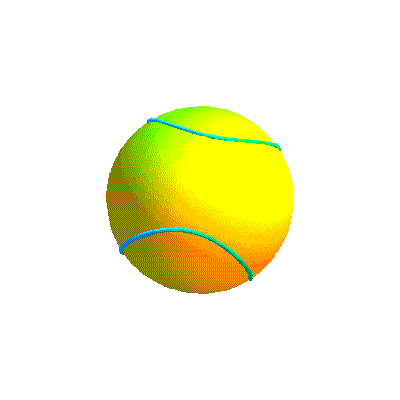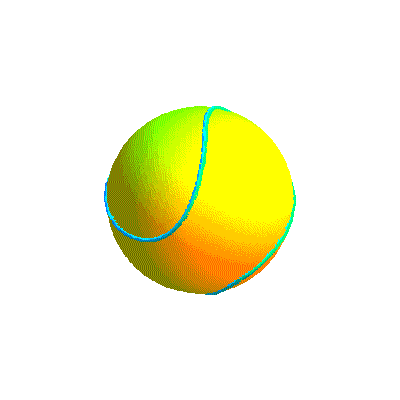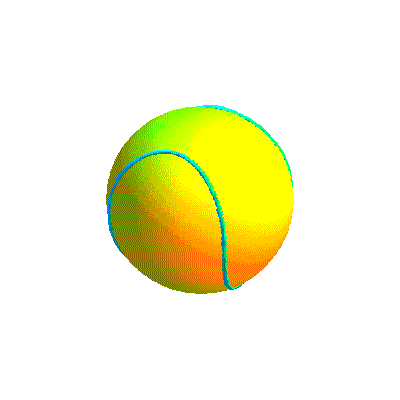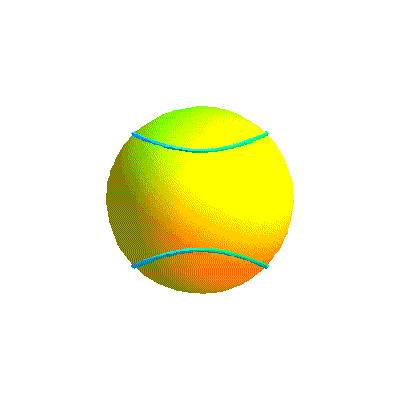

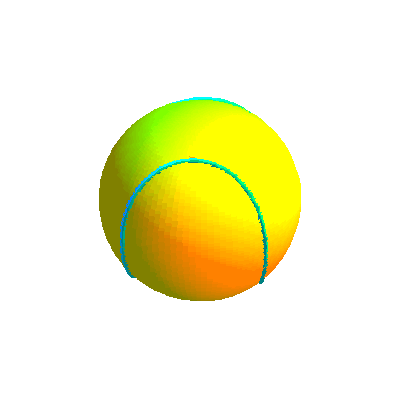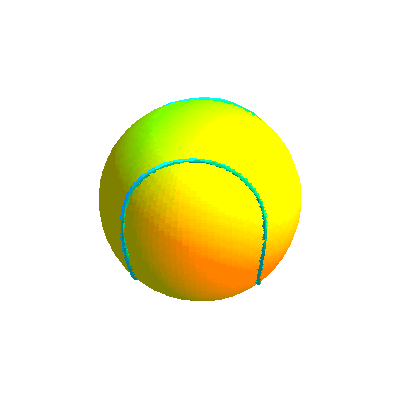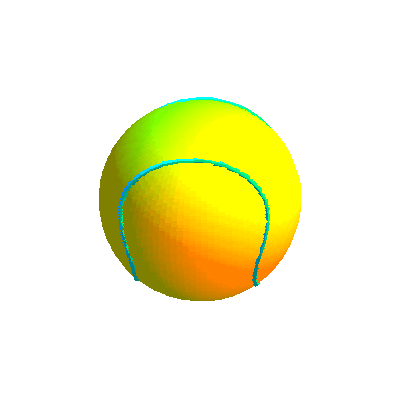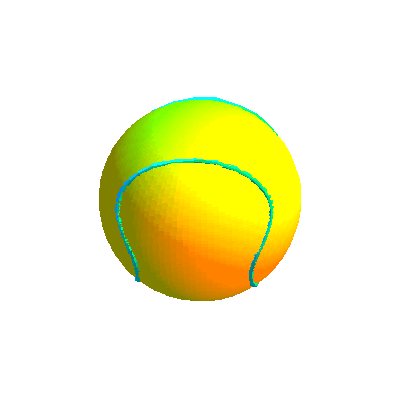
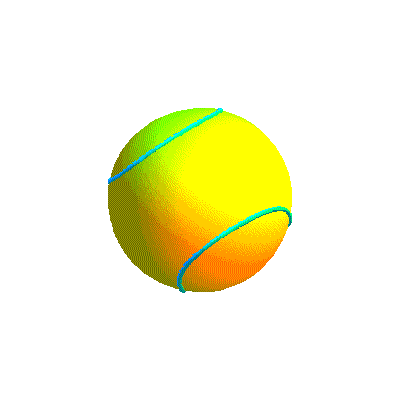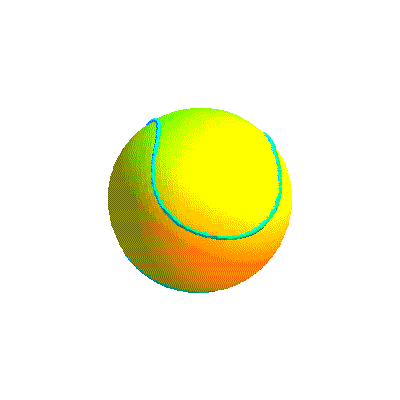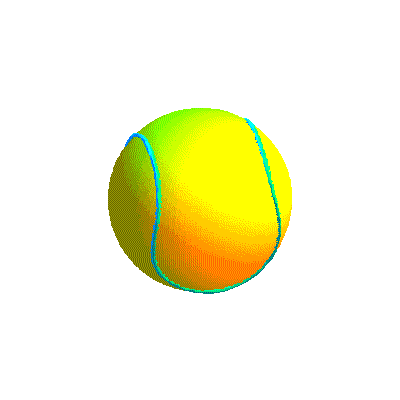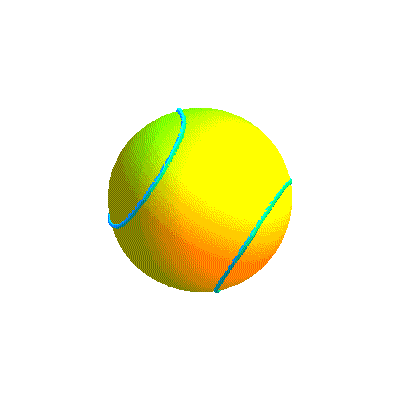
 Début
Début