I. Chemins auto-évitants sur différents réseaux

Les réseaux carré et losange donnent des résultats équivalents à une déformation près pour le graphisme.
Les réseaux hexagonal et mur de briques donnent des résultats équivalents à une déformation près pour le graphisme.
Le lien entre repérage et coordonnées d'un point du mur de brique est beaucoup plus simple à exprimer que pour le réseau en nid d'abeille.

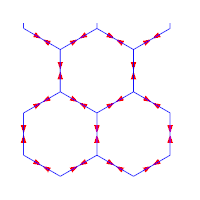
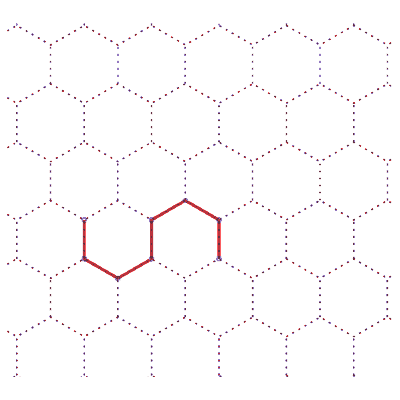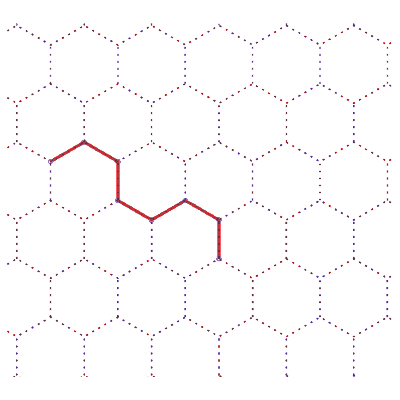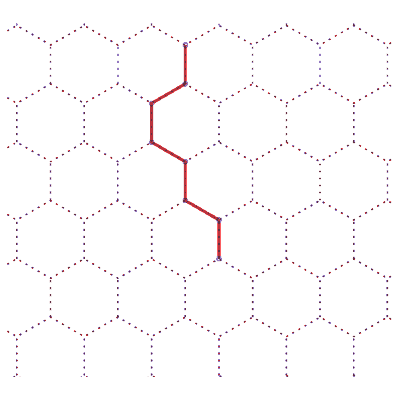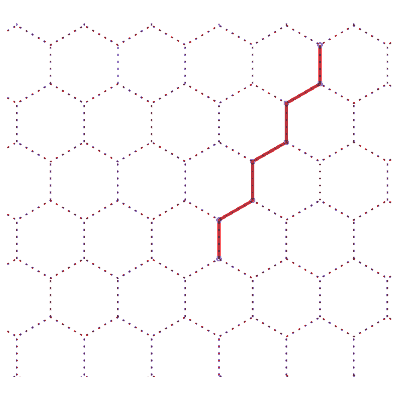
Réseau hexagonal ou en nid d'abeille
Sens de parcours sur le réseau	Un chemin aléatoire de longueur 99	18 différentes formes des chemins de longueur 7	nombre de chemins
			longueur 1 : 3 longueur 2 : 6 longueur 3 : 12 longueur 4 : 24 longueur 5 : 48 longueur 6 : 90 longueur 7 : 174 longueur 8 : 336 longueur 9 : 648 longueur 10 : 1218 longueur 11 : 2328
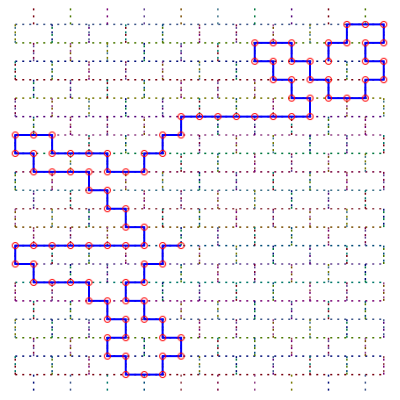
Réseau mur de briques
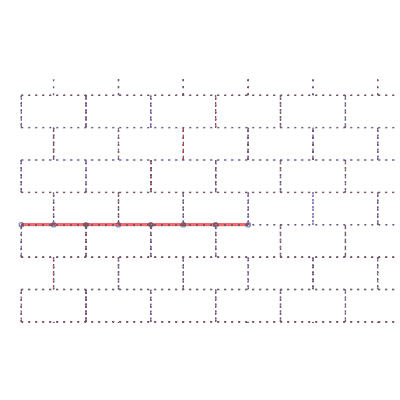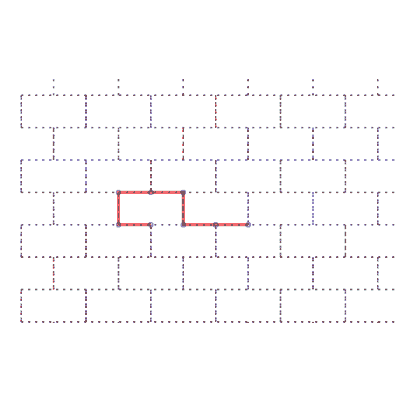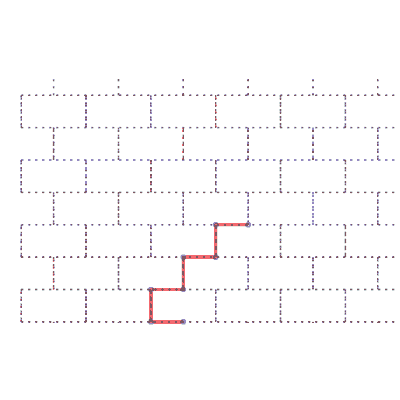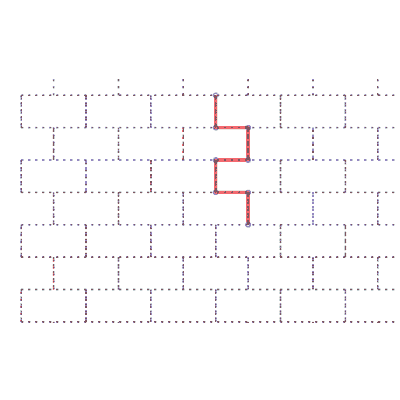
Sens de parcours sur le réseau	Un chemin aléatoire de longueur 99	18 différentes formes des chemins de longueur 7	nombre de chemins
			longueur 1 : 3 longueur 2 : 6 longueur 3 : 12 longueur 4 : 24 longueur 5 : 48 longueur 6 : 90 longueur 7 : 174 longueur 8 : 336 longueur 9 : 648 longueur 10 : 1218 longueur 11 : 2328
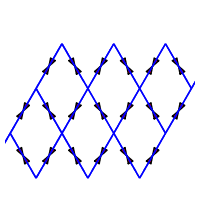
Réseau losange
Sens de parcours sur le réseau	Un chemin aléatoire de longueur 99	108 différentes formes des chemins de longueur 6	nombre de chemins
			longueur 1 : 4 longueur 2 : 12 longueur 3 : 36 longueur 4 : 100 longueur 5 : 284 longueur 6 : 780 longueur 7 : 2172 longueur 8 : 5916 longueur 9 : 16268
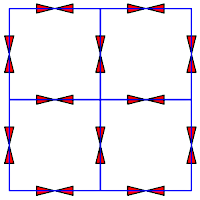
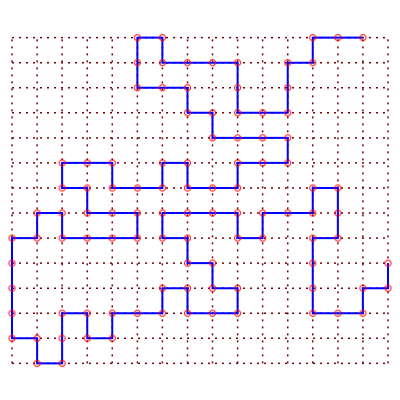
Réseau Carré
Sens de parcours sur le réseau	Un chemin aléatoire de longueur 99	56 différentes formes des chemins de longueur 6	nombre de chemins
			longueur 1 : 4 longueur 2 : 12 longueur 3 : 36 longueur 4 : 100 longueur 5 : 284 longueur 6 : 780 longueur 7 : 2172 longueur 8 : 5916 longueur 9 : 16268
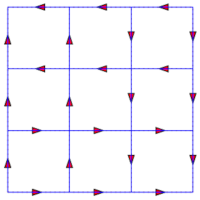
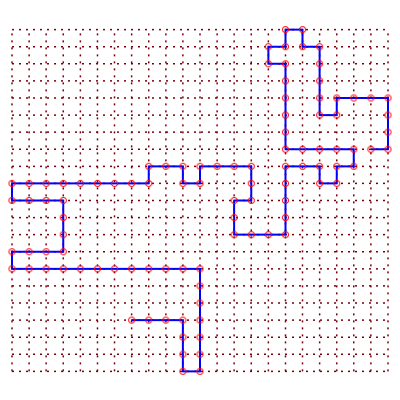
Réseau Carré orienté : lignes de même sens 2 par 2
Sens de parcours sur le réseau	Un chemin aléatoire de longueur 99	23 différentes formes des chemins de longueur 6	nombre de chemins
			longueur 1 : 2 longueur 2 : 4 longueur 3 : 8 longueur 4 : 16 longueur 5 : 30 longueur 6 : 58 longueur 7 : 110 longueur 8 : 202 longueur 9 : 382
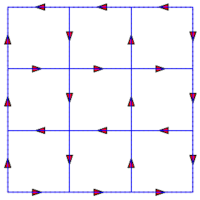
Réseau Carré orienté : lignes de même sens alterné
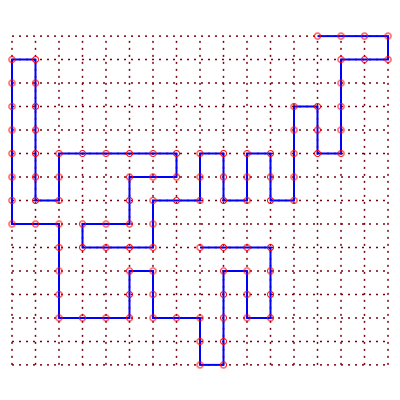
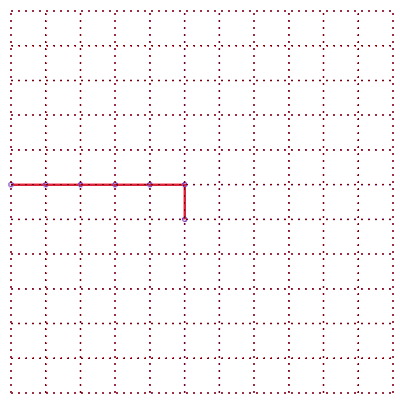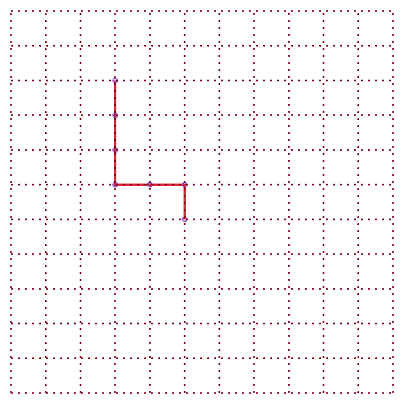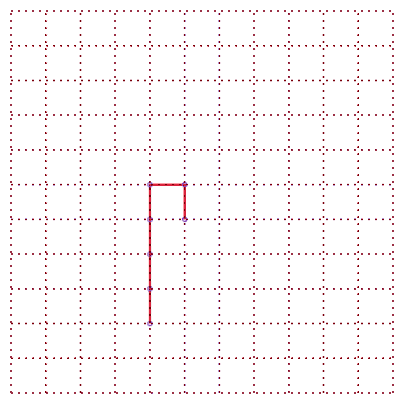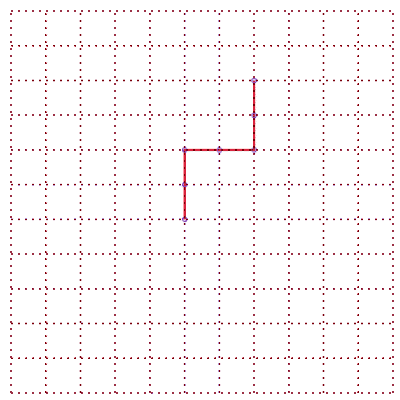
Sens de parcours sur le réseau	Un chemin aléatoire de longueur 99	15 différentes formes des chemins de longueur 6	nombre de chemins
			longueur 1 : 2 longueur 2 : 4 longueur 3 : 8 longueur 4 : 14 longueur 5 : 26 longueur 6 : 46 longueur 7 : 88 longueur 8 : 154 longueur 9 : 278
Réseau Carré orienté en L
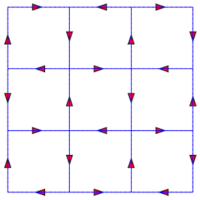
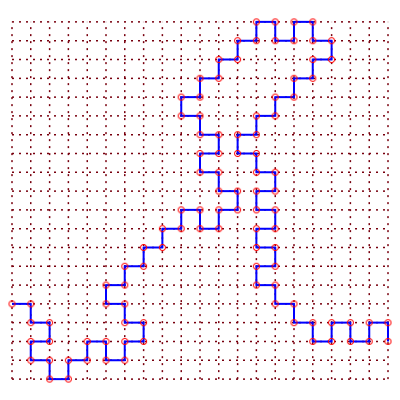
Sens de parcours sur le réseau	Un chemin aléatoire de longueur 99	5 différentes formes des chemins de longueur 6	nombre de chemins
			longueur 1 : 2 longueur 2 : 4 longueur 3 : 8 longueur 4 : 12 longueur 5 : 20 longueur 6 : 32 longueur 7 : 52 longueur 8 : 84 longueur 9 : 136
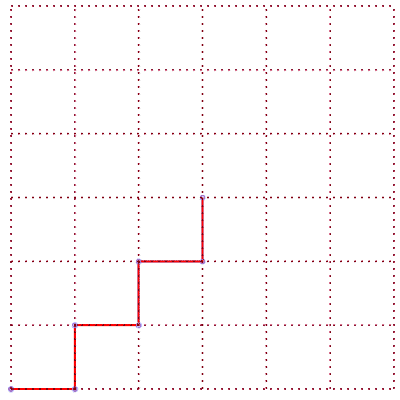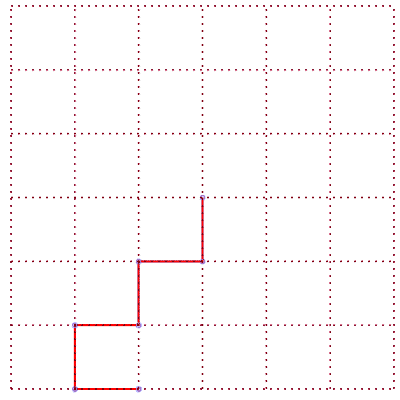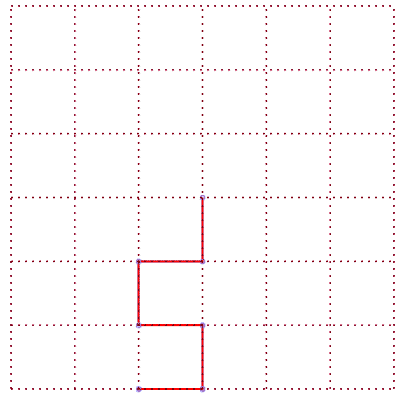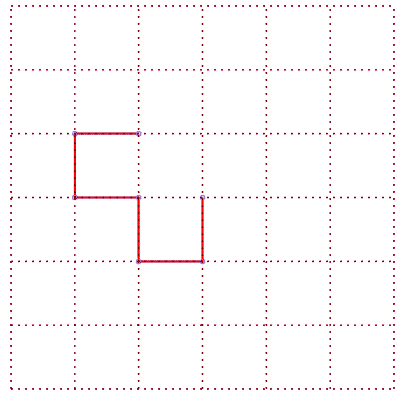Réseau triangulaire
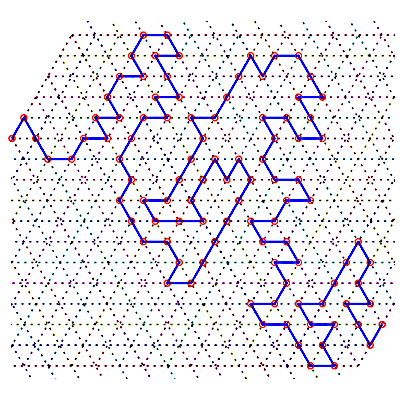
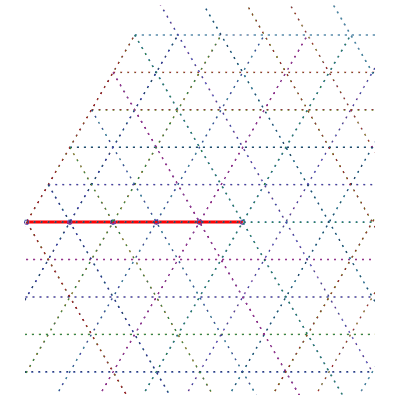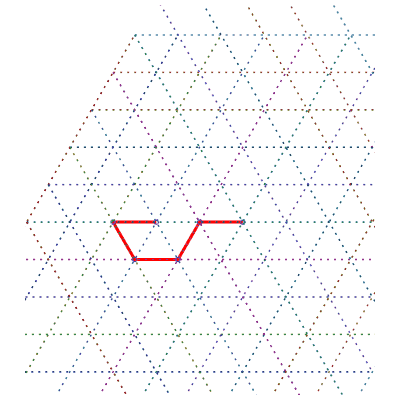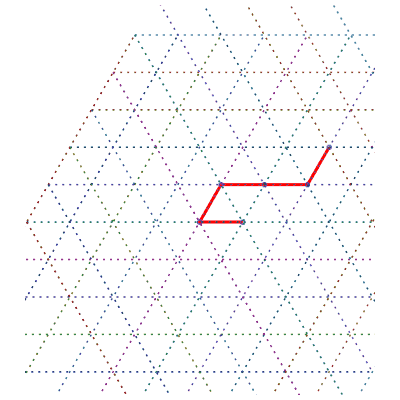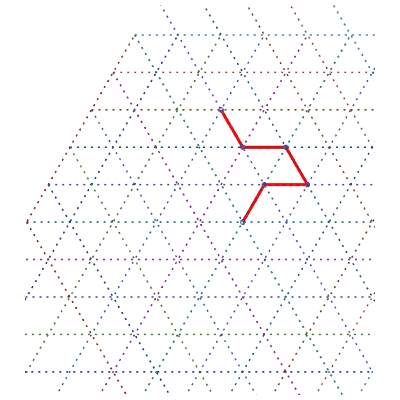
Sens de parcours sur le réseau	Un chemin aléatoire de longueur 99	293 différentes formes des chemins de longueur 6	nombre de chemins
			longueur 1 : 6 longueur 2 : 30 longueur 3 : 138 longueur 4 : 618 longueur 5 : 2730 longueur 6 : 11946 longueur 7 : 51882
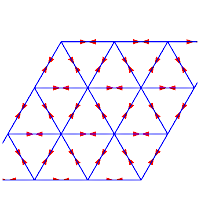Réseau triangulaire orienté
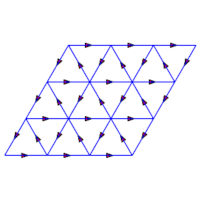
Sens de parcours sur le réseau	Un chemin aléatoire de longueur 99	52 différentes formes des chemins de longueur 6	nombre de chemins
			longueur 1 : 3 longueur 2 : 9 longueur 3 : 21 longueur 4 : 51 longueur 5 : 123 longueur 6 : 285 longueur 7 : 669

II. Chemins et cycles hamiltoniens sur un rectangle de NxM points

On considère un rectangle de NxM points et on recherche les chemins et cycles hamiltoniens remplissants ce rectangle.
J'ai codé un point [i,j] par 10*i+j ce qui suffit pour N et M inférieurs à 9 ( sinon on remplace 10 par 100 par exemple ), ce qui permet de manipuler des listes d'entiers au lieu de listes de liste.
Le tableau suivant présente quelques chemins et cycles pour des valeurs de N et M.

4x4
4x5
5x6

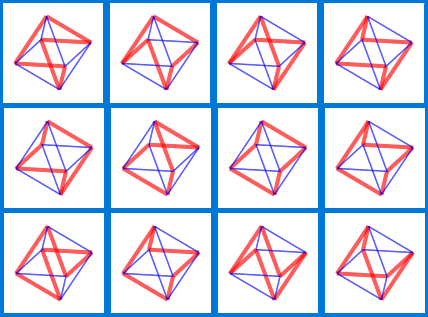
Les cycles hamiltoniens sur un octaèdre :
Le programme s'adapte très facilement pour trouver les chemins et cycles hamiltoniens sur un polyèdre : ci-dessous, l'octaèdre.

Début