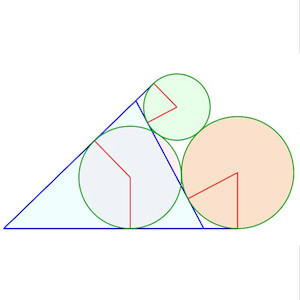
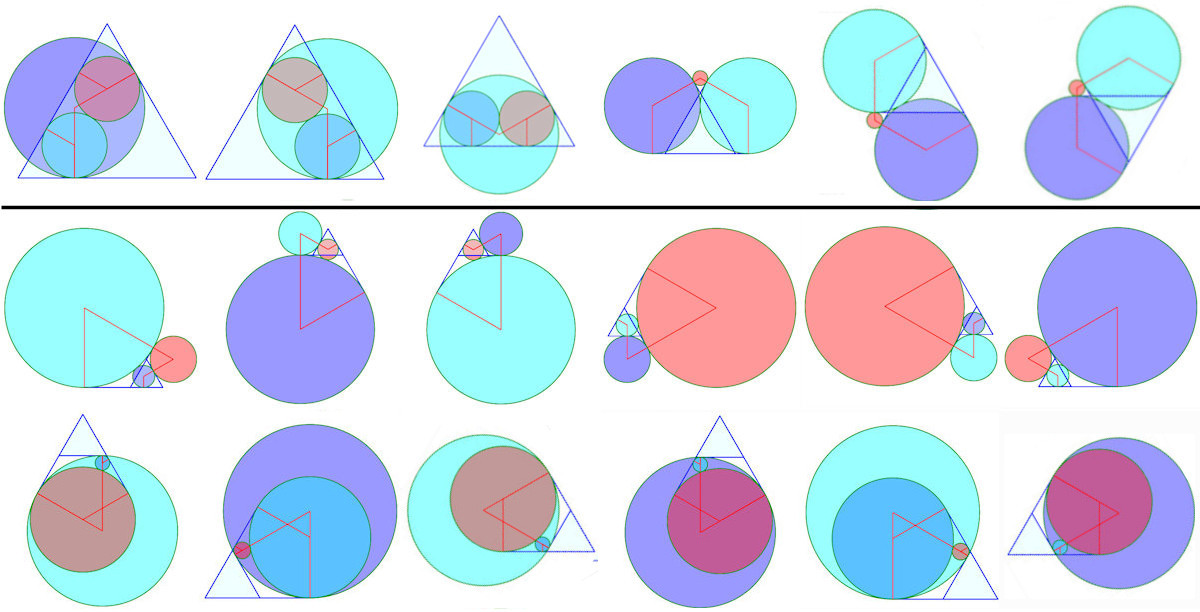
Solution "courante" à 9 contacts simples
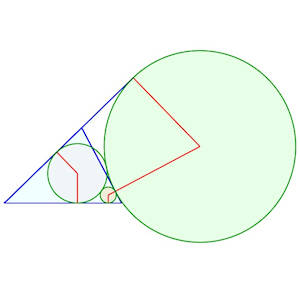
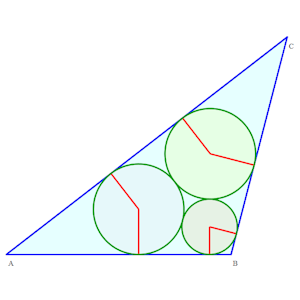
Solution à 1 contact triple, 6 simples
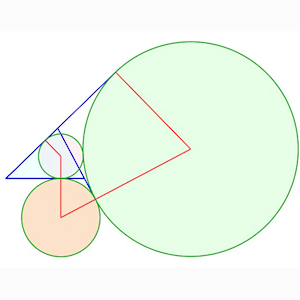
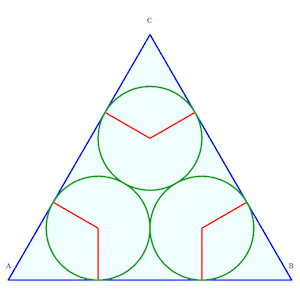
Solution à 2 contacts triples, 3 simples
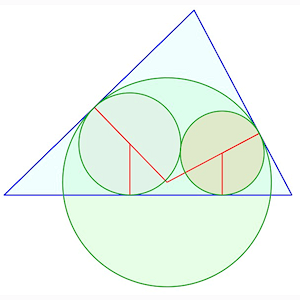
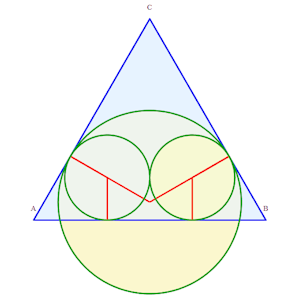
Solution à 2 contacts triples, 3 simples
Cercles de Malfatti généralisés
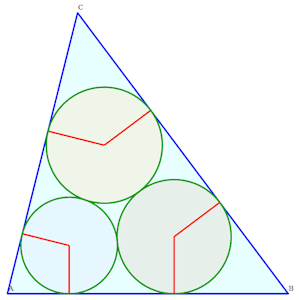
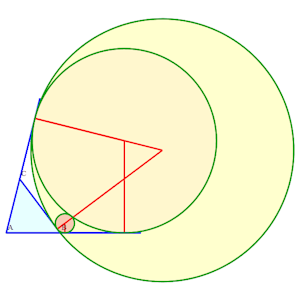
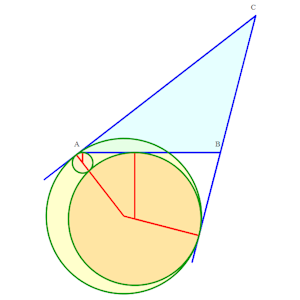
 Solution "courante" à 9 contacts simples |
 Solution à 1 contact triple, 6 simples |
 Solution à 2 contacts triples, 3 simples |
 Solution à 2 contacts triples, 3 simples |
|
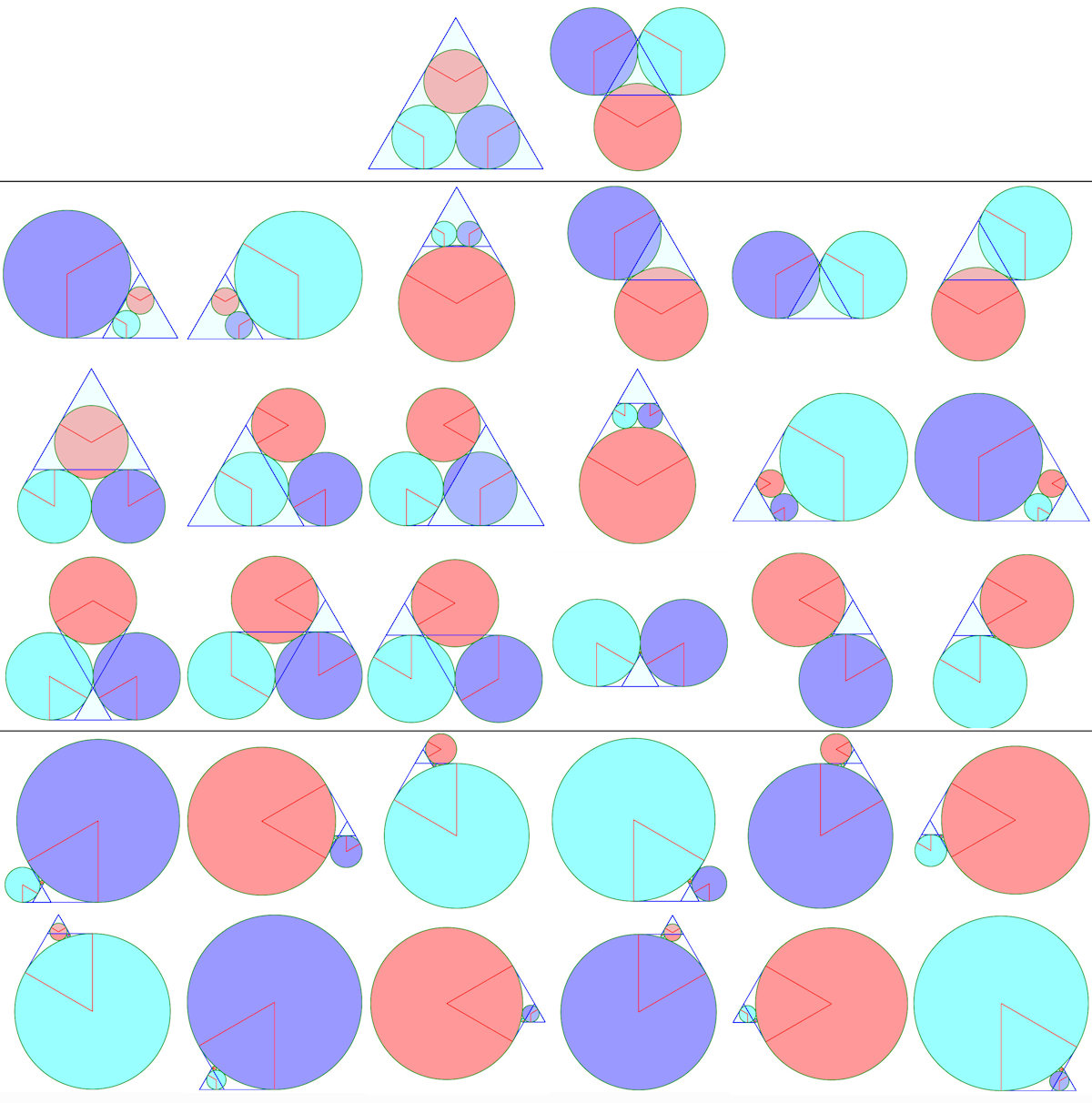
| |
|
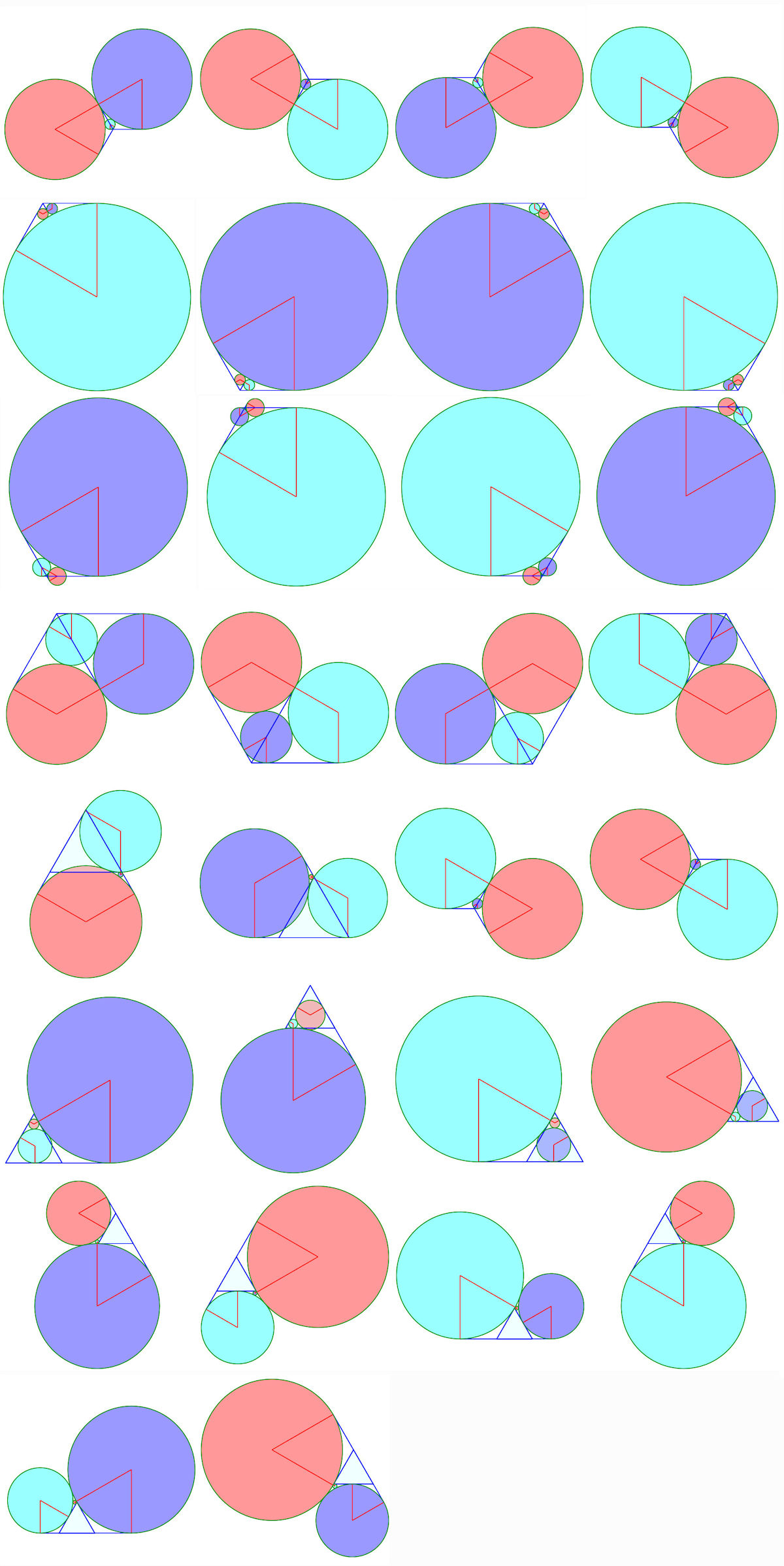
| |
|
|
|